Những câu hỏi liên quan
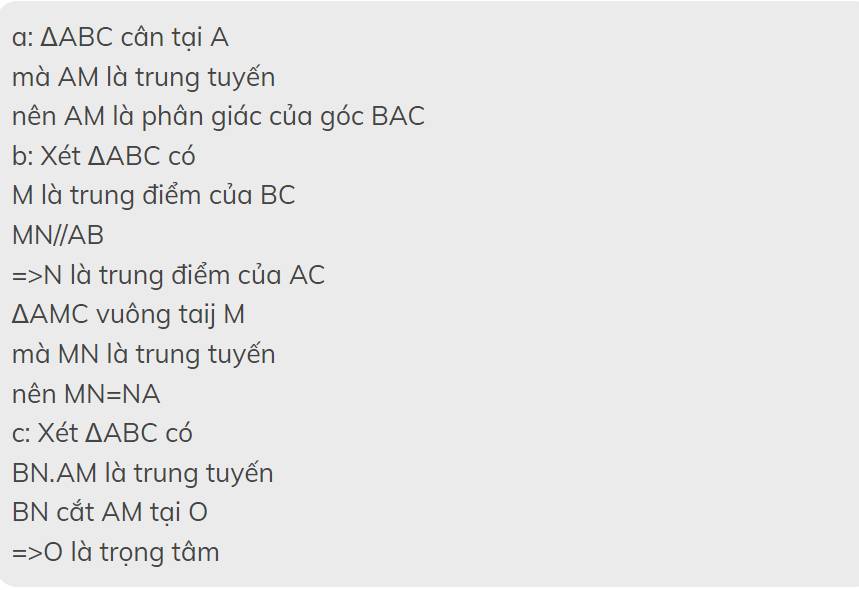
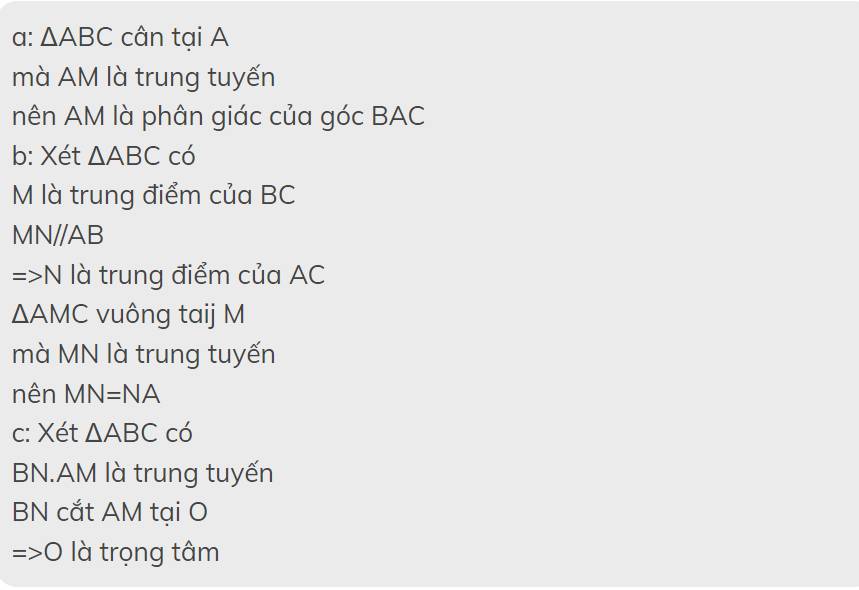
Cho tam giác ABC cân tại A , trung tuyến AM . Từ M kẻ MN // AB ( N Thuộc AC) , BN cắt AM tại O . a) CMR: AM là tia phân giác của BAC a) CMR: AN=NM b) CMR : O là trọng tâm của tam giác ABC Giúp e vs ạ e cảm ơn
Xem chi tiết
Cho tam giác ABC cân tại A , trung tuyến AM . Từ M kẻ MN // AB ( N AC) , BN cắt AM tại O . a) CMR: AM là tia phân giác của BAC a) CMR: AN=NM b) CMR : O là trọng tâm của tam giác ABC Giúp e vs ạ e cảm ơn
Xem chi tiết
Cho tam giác ABC cân tại A , trung tuyến AM . Từ M kẻ MN // AB , BN cắt AM tại O .
a) CMR: AN=NM
b) CMR : O là trọng tâm của tam giác ABC
Bài 5: Cho tam giác ABC, trung tuyến AM. Từ M kẻ đường thẳng song song với AB cắt AC tại N. Biết AN=MN; BN cắt AM ở O. Chứng minh:
a) Tam giác ABC cân ở A
b) O là trọng tâm của tam giác ABC
a,Xét ΔΔAMN có : AN=NM
⇒⇒góc NAM =góc NMA
mà góc NMA= góc MAB (vì MN song song với AB)
nên góc NAM =góc MAB hay MA là tia phân giác góc BAC
Xét ΔΔABC ta có:
AM là tia phân giác góc BAC và cũng là đường trung tuyến ứng với cạnh BC
⇒⇒ΔΔABC cân tại A
b, Theo câu a ta có :ΔΔABC cân tại A
⇒⇒góc ABC = góc NCM
Mà góc NMC = góc ABC
NÊN góc NMC= góc NCM
⇒⇒ ΔΔNMC cân tại N
⇒⇒MN=NC
mà NM=AN
Nên AN=NC hay BN là đường trung tuyến ứng với cạnh AC
Ta có: AM là đường trung tuyến ứng với cạnh BC
BN là đường trung tuyến ứng với cạnh AC
mà BN cắt AM tại O
Nên O là trọng tâm của tam giác ABC
a,Xét ΔΔAMN có : AN=NM
⇒⇒góc NAM =góc NMA
mà góc NMA= góc MAB (vì MN song song với AB)
nên góc NAM =góc MAB hay MA là tia phân giác góc BAC
Xét ΔΔABC ta có:
AM là tia phân giác góc BAC và cũng là đường trung tuyến ứng với cạnh BC
⇒⇒ΔΔABC cân tại A
b, Theo câu a ta có :ΔΔABC cân tại A
⇒⇒góc ABC = góc NCM
Mà góc NMC = góc ABC
NÊN góc NMC= góc NCM
⇒⇒ ΔΔNMC cân tại N
⇒⇒MN=NC
mà NM=AN
Nên AN=NC hay BN là đường trung tuyến ứng với cạnh AC
Ta có: AM là đường trung tuyến ứng với cạnh BC
BN là đường trung tuyến ứng với cạnh AC
mà BN cắt AM tại O
Nên O là trọng tâm của tam giác ABC
Đúng 2
Bình luận (0)
.1.Cho tam giác ABC cân tại A có AD là đường phân giác. a) Chứng minh tam giác ABD tam giác ACDb) Gọi G là trọng tâm tam giác ABC. Chứng minh ba điểm A, G, D thẳng hàng.c) Tính DG biết AB 13cm,BC 10cm2.Cho tam giác ABC vuông ở A, có AB 16cm,AC 30cm. Tính tổng các khoảng cách từ trọng tâm G của tam giác đến các đỉnh của tam giác.3.Cho tam giác ABC, trung tuyến AM. Từ M kẻ đường thẳng song song với AB cắt C ở N. Biết AN MN, BN cắt AM ở O. Chứng minh: a) Tam giác ABC cân ở Ab) O là trọng tâm t...
Đọc tiếp
.1.Cho tam giác ABC cân tại A có AD là đường phân giác.
a) Chứng minh tam giác ABD = tam giác ACD
b) Gọi G là trọng tâm tam giác ABC. Chứng minh ba điểm A, G, D thẳng hàng.
c) Tính DG biết AB 13cm,BC 10cm
2.Cho tam giác ABC vuông ở A, có AB = 16cm,AC = 30cm. Tính tổng các khoảng cách từ trọng tâm G của tam giác đến các đỉnh của tam giác.
3.Cho tam giác ABC, trung tuyến AM. Từ M kẻ đường thẳng song song với AB cắt C ở N. Biết AN = MN, BN cắt AM ở O. Chứng minh: a) Tam giác ABC cân ở A
b) O là trọng tâm tam giác ABC.
4.Cho tam giác cân ABC, trung tuyến AM. Đường trung trực của AB cắt AM ở O. Chứng minh rằng điểm O cách đều 3 đỉnh của tam giác ABC.
Cần gấp ạ!
Cho △ABC cân tại A, trung tuyến AM. Từ M kẻ MN//AB (N∈AC), BN cắt AM tại O
a) CMR: AN=NM
b) CMR: O là trọng tâm △ABC
Cho tam giác ABC trung tuyến AM. Từ M kẻ đường thẳng song song với AB cắt AC ở N. Biết AN=MN, BN cắt AM ở O. Chứng minh:
a) tam giác ABC cân ở A
b) O là trọng tâm của tam giác ABC
Cho tam giác ABC cân tại A có AM là trung tuyến và AM = 6cm; BC=4cm
a) CMR: AM là p/g của góc BAC AM là trug trực của BC
b) Lấy điểm O trên AM sao cho AO = 4cm. Nối BO cắt AC tại E. CMR E là trung trực của AC
c) Nối CO cắt AB tại F. CMR BE = CF
d) Tính BO, CO và góc OBC
* Giúp e vs ạ đc bao nhiu thì đc ạ
a: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM vừa là đường phân giác vừa là đường cao
b: Xét ΔABC có
AM là đường trung tuyến
AO=2/3AM
Do đó: O là trọng tâm của ΔABC
=>BO là đường trung tuyến ứng với cạnh AC
hay E là trung điểm của AC
c: Ta có: O là trọng tâm của ΔABC
mà CO cắt BA tại F
nên F là trung điểm của AB
Xét ΔABE và ΔACF có
AB=AC
\(\widehat{BAE}\) chung
AE=AF
Do đó: ΔABE=ΔACF
Suy ra: BE=CF
Đúng 1
Bình luận (0)
1. Cho tam giác ABC, trung tuyến AM. Kẻ BH, CK vuông góc với AM. Gọi E là trung điểm của BK, F là trung điểm của CH. CMR tam giác AEF cân2. Cho tam giác ABC cân tại A( góc A nhỏ hơn 45 độ), lấy M thuộc BC. Từ M kẻ MH song song AB(H thuộc AB) , kẻ MI song song AC( I thuộc AC). Lấy N sao cho HI là trung trực của MN. Gọi giao điểm của NH và AB là D. CMR: chu vi tam giác ADH không phụ thuộc vào vị trí điểm M3. Cho tam giác ABC, trung tuyến AM. Trên tia AM lấy điểm N sao cho MNAM. Dựng ra...
Đọc tiếp
1. Cho tam giác ABC, trung tuyến AM. Kẻ BH, CK vuông góc với AM. Gọi E là trung điểm của BK, F là trung điểm của CH. CMR tam giác AEF cân
2. Cho tam giác ABC cân tại A( góc A nhỏ hơn 45 độ), lấy M thuộc BC. Từ M kẻ MH song song AB(H thuộc AB) , kẻ MI song song AC( I thuộc AC). Lấy N sao cho HI là trung trực của MN. Gọi giao điểm của NH và AB là D. CMR: chu vi tam giác ADH không phụ thuộc vào vị trí điểm M
3. Cho tam giác ABC, trung tuyến AM. Trên tia AM lấy điểm N sao cho MN=AM. Dựng ra ngoài tam giác ABC các tam giác ABD và tam giác ACE vuông cân tại A.
A, CMR: BE vuông góc CD
B, CMR: AN= DE và AN vuông góc với DE