Cho điểm A(-1:-1) B(-5;3) viết phương trình đường thẳng trung trực đường thẳng AB

Những câu hỏi liên quan
cho các điểm A(0,-5),B(-1,-1),C(2,1),D(\(\dfrac{5}{2}\),\(\dfrac{5}{2}\))
a) Tìm a, b đề đường thẳng
y=ax+b đi qua hai điểm A và B.
b) Chứng minh 4 điểm A, B, C, D thẳng hàng
a.
Gọi d là đường thẳng đi qua A, B. Do A; B đều thuộc d nên tọa độ A; B phải thỏa mãn pt d
\(\Leftrightarrow\left\{{}\begin{matrix}-5=a.0+b\\-1=-1.a+b\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-4\\b=-5\end{matrix}\right.\)
b.
Câu b đề sai, 4 điểm này không hề thẳng hàng (thay tọa độ C, D vào pt d đều không thỏa mãn)
Đúng 3
Bình luận (0)
Cho 4 điểm A ( 0; -5) , B (-5 ;20 ) , C( 2 ; 1) , D( 2 ; 5 )
Cmr : 4 điểm A , B, C thẳng hàng
b. Tìm x sao cho 3 điểm A( x ; 14) , B( -5 ; 20 ) , C( 7 ; -16)
Cho A(2; 5); B(1; 3) và C(5; -1). Tìm tọa độ điểm K sao cho A. (-4; -4). B. (-4; 5). C. (5; -4). D. (-5; -4).
Đọc tiếp
Cho A(2; 5); B(1; 3) và C(5; -1). Tìm tọa độ điểm K sao cho ![]()
A. (-4; -4).
B. (-4; 5).
C. (5; -4).
D. (-5; -4).
Chọn B.
Gọi K(x; y).
Khi đó
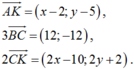
Theo đầu bài ![]() nên
nên
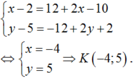
Đúng 0
Bình luận (0)
Cho 2 điểm A(1; 3; 5), B(1; -1; 1) khi đó trung điểm I của AB có tọa độ là
A. I(0; -4; -4)
B. I(2; 2; 6)
C. I(0; -2; -4)
D. I(1; 1; 3)
Cho ba điểm A(0; 1), B(1; 2), C(-5; -4).
a)Viết phương trình đường thẳng d đi qua hai điểm A và B.
b) Chứng minh ba điểm A, B, C thẳng hàng.
Lời giải:
a. Gọi ptdt $(d)$ đi qua $A,B$ là $y=ax+b$
Ta có: \(\left\{\begin{matrix} y_A=ax_A+b\\ y_B=ax_B+b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 2=a+b\\ 1=a.0+b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} b=1\\ a=1\end{matrix}\right.\)
Vậy ptđt $(d)$ là: $y=x+1$
b. Ta thấy: $y_C=-4=-5+1=x_C+1$ nên $C\in (d): y=x+1$
Tức là $C$ thuộc đt đi qua 2 điểm $A,B$
$\Rightarrow A,B,C$ thẳng hàng.
Đúng 0
Bình luận (0)
cho ba điểm A(1;-5),B(-1;-2),C(x,6).Tìm x để A,B,C thẳng hàng
cho ba điểm A,B,C có các tọa độ A(1,-1),B(2,3),C(3,-5) Tìm tọa độ điểm M sao cho vecto AM-2AB+4AC=0 giúp mk với 😫😫
Cho hàm số y = ax + b .Tìm a và b, biết rằng đồ thị của hàm số đã cho thỏa mãn một trong các điều kiện sau:
a) Đi qua hai điểm A(1; 3) và B(-1; -1).
b) Song song với đường thẳng y = x + 5 và đi qua điểm C(1; 2).
a) Đồ thị hàm số y = ax + b đi qua A(1; 3) và B(-1; -1)
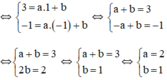
Vậy a = 2; b = 1; hàm số y = 2x + 1.
b) y = ax + b song song với y = x + 5
⇒ a = 1.
Đồ thị hàm số đi qua C(1; 2) ⇔ 2 = a.1 + b ⇔ a + b = 2 ⇒ b = 1.
Vậy a = 1; b = 1.
Đúng 0
Bình luận (0)
Cho hàm số y = ax + b .Tìm a và b, biết rằng đồ thị của hàm số đã cho thỏa mãn một trong các điều kiện sau:
a) Đi qua hai điểm A(1; 3) và B(-1; -1).
b) Song song với đường thẳng y = x + 5 và đi qua điểm C(1; 2).
a) Đồ thị hàm số y = ax + b đi qua A(1; 3) và B(-1; -1)
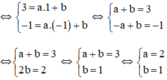
Vậy a = 2; b = 1; hàm số y = 2x + 1.
b) y = ax + b song song với y = x + 5
⇒ a = 1.
Đồ thị hàm số đi qua C(1; 2) ⇔ 2 = a.1 + b ⇔ a + b = 2 ⇒ b = 1.
Vậy a = 1; b = 1.
Đúng 0
Bình luận (0)
Cho đường thẳng delta x-2y+1=0 và 2 điểm A(6;5), B(-4;1). Biết điểm P (a;b) thuộc đg thẳng delta thõa mản PA+PB ngắn nhất. Tính S= a+b
A. S=-1
B. S =5
C. S=-5
D. S= 1











