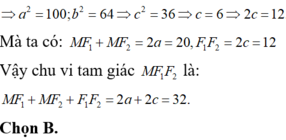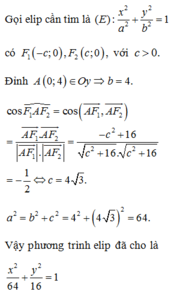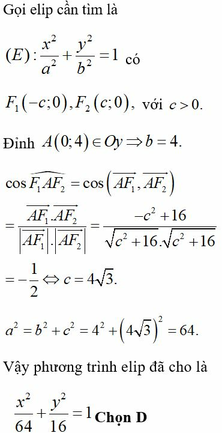Elip x2/16+y2/9=1 có hai tiêu điểm F1, F2; M là một điểm bất kì nằm trên elip. Tính MF1+MF2 A.10. B.8 C.6 D.12

Những câu hỏi liên quan
câu 23:Elip có hai đỉnh là -3,0;3,0 và có hai tiêu điểm là (-1,0);(1,0).Phương trình chính tắc của elip là :A.x2/9+y2/1=1,B.x2/8+y2/9=1,c.x2/36+y2/8=1,D.x2/24+y2/16=
Từ giả thiết suy ra:\(a^2=9\),\(c^2=1\) ,
-- > \(b^2=c^2-a^2=8\)
Vậy pt chính tắc của elip là : \(\dfrac{x^2}{9}+\dfrac{y^2}{8}=1\)
Ta chọn C
Đúng 1
Bình luận (0)
Cho elip
E
:
x
2
25
+
y
2
9
1
có hai tiêu điểm
F
1
;
F
2
. Hai điểm M, N phân biệt thuộc elip
E
thỏa mãn
M
F
1
+
N...
Đọc tiếp
Cho elip E : x 2 25 + y 2 9 = 1 có hai tiêu điểm F 1 ; F 2 . Hai điểm M, N phân biệt thuộc elip E thỏa mãn M F 1 + N F 2 = 14 . Tính giá trị của biểu thức M F 2 + N F 1
A. M F 2 + N F 1 = 2
B. M F 2 + N F 1 = 4
C. M F 2 + N F 1 = 8
D. M F 2 + N F 1 = 6
Chọn đáp án D

MEMORIZE |
Định nghĩa đường elip, phương trình chính tắc của elip. |
Đúng 0
Bình luận (0)
Cho elip (E): x 2 + 9 y 2 = 9
a) Tìm tọa độ hai tiêu điểm của elip
b) Tìm trên (E) điểm M sao cho MF1 = 2MF2
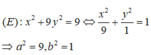
Ta có: c2 = a2 - b2 = 9 - 1 = 8 ⇒ c = 2√2
⇒ F1(-2√2;0), F2(2√2;0)
Tìm trên (E) điểm M sao cho MF1 = 2MF2
Giả sử M(x;y) là điểm thỏa mãn yêu cầu của đề bài
Vì M thuộc (E) nên:
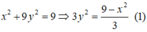
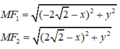
Theo đề bài ta có:
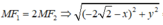
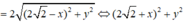
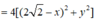
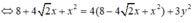
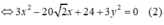
Thay (1) vào (2) ta được:
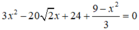
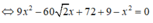
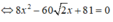
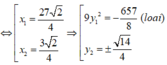
Vậy có hai điểm thỏa mãn đề bài là:
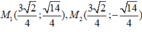
Đúng 0
Bình luận (0)
Cho elip có phương trình
x
2
100
+
y
2
64
1
Với hai tiêu điểm F1 và F2 với một điể M bất kì nằm trên elip thì chu vi tam giác MF1F2 là A. 16 B. 32 C. 36 D. 72
Đọc tiếp
Cho elip có phương trình x 2 100 + y 2 64 = 1 Với hai tiêu điểm F1 và F2 với một điể M bất kì nằm trên elip thì chu vi tam giác MF1F2 là
A. 16
B. 32
C. 36
D. 72
cho elip (e) có pt chính tắc: x^2/9 + y^2/4=1
a) tìm tọa độ đỉnh, tiêu điểm f1, f2, và tâm sai của (e)
b) tìm tọa độ điểm m thuộc (e) thõa mãn mf1 -mf2=2
(f1 là tiêu điểm bên trái của elip)
Cho elip (E) có phương trình
x
2
169
+
y
2
25
1
với hai tiêu điểm là
F
1
,
F
2
. Với điểm M bất kì trên (E) thì chu vi tam giác
M
F
1
F
2
là: A. 50 B. 36 C. 34 D. Thay đổi phụ thuộc vào vị...
Đọc tiếp
Cho elip (E) có phương trình x 2 169 + y 2 25 = 1 với hai tiêu điểm là F 1 , F 2 . Với điểm M bất kì trên (E) thì chu vi tam giác M F 1 F 2 là:
A. 50
B. 36
C. 34
D. Thay đổi phụ thuộc vào vị trí M
Từ phương trình chính tắc của (E) ta có các thông tin về các bán trục và bán tiêu cự a = 13, b = 5, c = 12.

Đúng 0
Bình luận (0)
Cho elip (E) có phương trình:
x
2
169
+
y
2
25
1
với hai tiêu điểm là F1, F2. Với điểm M bất kì trên (E) thì chu vi tam giác MF1F2 là: A. 50 B. 36 C. 34 D. Phụ thuộc vào vị trí của M
Đọc tiếp
Cho elip (E) có phương trình: x 2 169 + y 2 25 = 1 với hai tiêu điểm là F1, F2. Với điểm M bất kì trên (E) thì chu vi tam giác MF1F2 là:
A. 50
B. 36
C. 34
D. Phụ thuộc vào vị trí của M
Đáp án: A
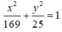
có a 2 = 169 ⇒ a = 13, b 2 = 25 ⇒ b = 5
c 2 = a 2 - b 2 = 169 - 25 = 144 ⇒ c = 12
Với điểm M bất kì thuộc elip ta có: MF1 + MF2 = 2a = 2.13 = 26
F1F2 = 2c = 2.12 = 24
Chu vi tam giác MF1F2: C = MF1 + MF2 + F1F2 = 26 + 24 = 50
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho elip có đỉnh A(0;4) nhìn hai tiêu điểm
F
1
,
F
2
dưới một góc bằng
120
°
. Phương trình chính tắc của elip đã cho là
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho elip có đỉnh A(0;4) nhìn hai tiêu điểm F 1 , F 2 dưới một góc bằng 120 ° . Phương trình chính tắc của elip đã cho là
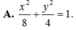
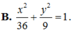
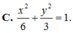
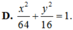
Trong mặt phẳng tọa độ Oxy, cho elip có đỉnh A(0;4) nhìn hai tiêu điểm
F
1
,
F
2
dưới một góc bằng
120
∘
. Phương trình chính tắc của elip đã cho là A.
x
2
8
+
y
2
4
1
B.
x...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho elip có đỉnh A(0;4) nhìn hai tiêu điểm F 1 , F 2 dưới một góc bằng 120 ∘ . Phương trình chính tắc của elip đã cho là
A. x 2 8 + y 2 4 = 1
B. x 2 36 + y 2 9 = 1
C. x 2 6 + y 2 3 = 1
D. x 2 64 + y 2 16 = 1