Cho lăng kính tam giác vuông cân ở A, n= chiếu tia tới song song mặt đáy gần B. Xác định đường đi của tia sáng
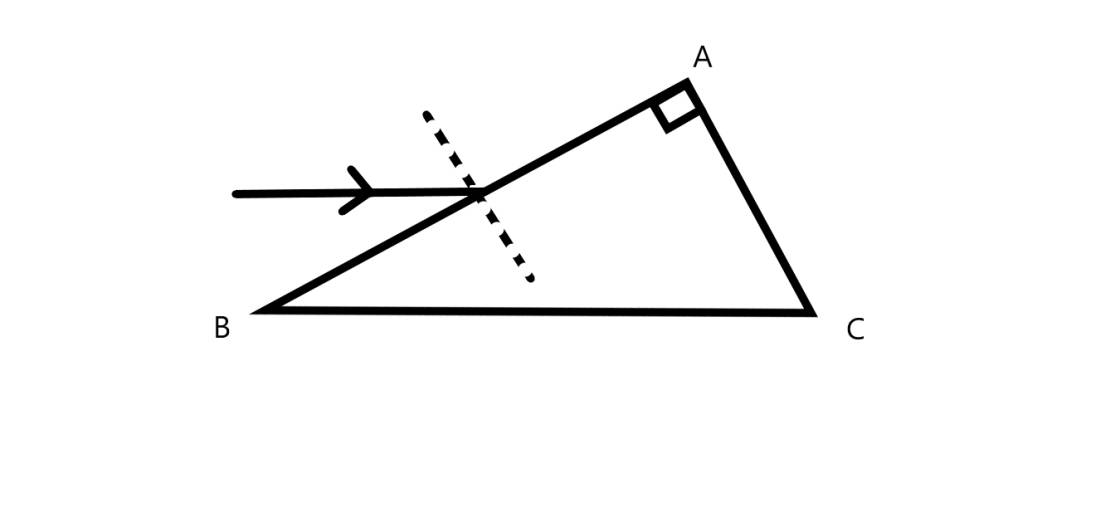
1 lăng kính thủy tinh có n=1,5, tiết diện là tam giác vuông cân ABC vuông tại A Tia sáng SI chiếu tới mặt phẳng AB theo phương song song với BC. Xác định đường đi của tia sáng qua lăng kính.
Một lăng kính thủy tinh có chiết suất n=1,5 tiết diện thẳng là tam giác vuông cân ABC, góc A=90. Chiếu tia sáng đến mặt bên lăng kính tại I sao cho nó song song với đáy BC. Tia khúc xạ qua mặt bên đến đáy BC tại K. Vẽ đường đi của tia sáng bằng việc tính các góc i, r, và tính góc lệch D?
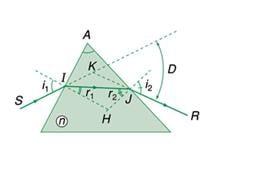
Sini1 = nsinr1 -->sin\(90^o\) = 1,5sinr1 --> r1 = 39,2 ;
r1 + r2 = A --> r2 = 50,8;
nsinr2 = sini2 --> 1,5sin39,2 = sini2 -->i2 = 58,8
Góc lệch của tia sáng qua lăng kính: D = i1 + i2 – A = 8\(^o\)
Một khối thủy tinh P có chiết suất n đặt trong không khí. Tiết diện thẳng là một tam giác cân ABC vuông tại B. Chiếu vuông góc tới mặt AB chùm sáng song song SI thì tia sáng đi là là mặt AC. Xác định chiết suất của khối chất P.
A. 3
B. 2
C. 1,5
D. 1,6
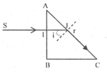
+ Vì tia SI đi vuông góc với mặt AB nên đi thẳng tới mặt bên AC với góc tới i.
+ Vì tam giác ABC vuông và cân tại B nên:

Chiếu một chùm tia sáng trắng hẹp song song coi như một tia sáng vào mặt bên AB (gần A) của lăng kính có góc chiết quang 300, theo phương vuông góc. Biết chiết suất của chất làm lăng kính đối với tia đỏ và tia tím lần lượt là: 1,532 và 1,5867. Sau lăng kính 1 (m) đặt một màn ảnh song song với mặt AB. Xác định khoảng cách giữa hai vệt sáng đỏ và tím trên màn.
A. 50 mm.
B. 1,2 mm.
C. 45 mm.
D. 44 mm.
Chọn đáp án A.
n d sin A = sin i d ⇒ 1 , 532 sin 30 0 = sin i d ⇒ i d ≈ 50 0 ⇒ D d = i d − A = 20 0 n t sin A = sin i t ⇒ 1 , 5867 sin 30 0 = sin i t ⇒ i t ≈ 52 , 5 0 ⇒ D t = i t − A = 22 , 5 0
D T = I O ( tan D t − tan D d ) = 1000 ( tan 22 , 5 0 − tan 20 0 ) ≈ 50 ( m m ) .
Chú ý: Nếu lăng kính có góc chiết quang bé và góc tới bé thì D = ( n − 1 ) A ⇒ D d = ( n d − 1 ) A D t = ( n t − 1 ) A
⇒ δ = D t − D d = ( n t − n d ) A
Độ rộng quang phổ lúc này: D T = I O ( tan D t − tan D d ) ≈ I O ( D t − D d ) = I O ( n t − n d ) A
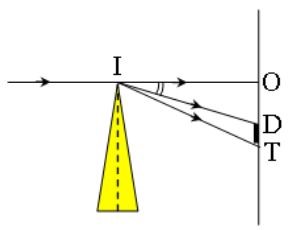
Cho một lăng kính có chiết suất 1,5 đặt trong không khí, tiết diện thẳng là một tam giác đều ABC. Trong mặt phẳng ABC, chiếu tới trung điểm của AB một chùm sáng hẹp, song song với góc tới 17°. Tia ló ra khỏi lăng kính lệch so với tia tới một góc gần giá trị nào nhất sau đây?
A. 95°
B. 22,5°
C. 45°
D. 90°
\(\left\{{}\begin{matrix}sin\left(i_{gh}\right)=\dfrac{1}{n}\xrightarrow[]{n=1,5}i_{gh}=41,81^o\\sin\left(i_1\right)=n.sin\left(r_1\right)\xrightarrow[i_1=17^o]{n=1,5}r_1=11,239^o\\r_1+r_2=A\xrightarrow[]{A=60^o}r_2=48,761^o>i_{gh}\\r_2+r_3=C\xrightarrow[]{C=60^o}11,239^o=r_1\end{matrix}\right.\)
\(n.sin\left(r_3\right)=sin\left(i_3\right)\Rightarrow i_3=17^o\)
Tia IJ quay theo chiều kim đồng hồ với góc SI một góc là:
\(D_1=17^o-11,239^o=5,761^o\)
Tia JK quay theo chiều kìm đồng hồ so với góc IJ một góc là:
\(D_2=180^o-2.48.761^o=82,478^o\)
Tia KR quay theo chiều kim đồng hồ so với góc JK là:
\(D_3=17^o-11,239^o=5,761^o\)
Vậy tia ló lệch tia tới:
\(D_1+D_2+D_3=94^o\)
⇒ Chọn A
Một lăng kính có góc chiết quang A=60, chiếu một chùm tia tới song song hẹp màu lục vào cạnh bên của lăng kính theo phương vuông góc với mặt phân giác của góc A sao cho một phần của chùm tia sáng không đi qua lăng kính và một phần qua lăng kính. Biết chiết xuất của lăng kính đối với ánh sáng màu lục n =1,55. Khi i, A bé thì góc lệch D của tia sáng qua lăng kính là:
A. 2,860
B. 2,750
C. 3,30
D. 2,570
Phương pháp: Áp dụng công thức tính góc lệch giữa tia tới và tia ló khi lăng kính có góc chiết quang nhỏ
Cách giải: Áp dụng công thức tính góc lệch ta có:
D = (n-1)A = (1,55-1). 6 0 = 3 , 3 0
Đáp án C
Cho một lăng kính có chiết suất 1,5 đặt trong không khí, tiết diện thẳng là một tam giác đều ABC. Trong mặt phẳng ABC, chiếu tới trung điểm của AB một chùm sáng hẹp, song song với góc tới 15 ° . Tia ló ra khỏi lăng kính lệch so với tia tới một góc gần giá trị nào nhất sau đây?
A. 30 °
B. 22 , 5 °
C. 45 °
D. 90 °
Chiếu một tia sáng đơn sắc đến mặt bên AB của một lăng kính tiết diện là một tam giác đều ABC theo phương song song với đáy BC. Tia ló ra khỏi AC đi là là mặt AC. Chiết suất của chất làm lăng kính là:
A. 2
B. 1,8
C.1,53
D. 3
Đáp án cần chọn là: C
Vì ∆ABC là tam giác đều và tia tới đi song song với cạnh đáy BC nên dễ suy ra được i 1 = 30 0 .
Mà: sin i 1 = n sinr 1 ↔ sin 30 0 = n sinr 1 → n sinr 1 = 0,5 (1)
Tia ló đi là là mặt AC, nên i 2 = 90 0
Góc chiết quang: A = r 1 + r 2
Ta lại có:
sin i 2 = n sinr 2 ↔ sin 90 = n sin ( A − r 1 )
↔ sin 90 = n sin ( 60 − r 1 ) ( 2 )
Lấy (2) chia cho (1) ta được:
sin 90 0,5 = n sin ( 60 − r 1 ) n sinr 1 ↔ 2 s i n r 1 = s i n ( 60 − r 1 )
↔ 2 sin r 1 = sin 60 c osr 1 − c os 60 sinr 1
↔ ( 2 + c os 60 ) sinr 1 = sin 60. c osr 1
→ tanr 1 = sin 60 2 + c os 60 = 3 5 → r 1 = 19,1 0
Thay vào (1), ta được: n = 0,5 sinr 1 = 0,5 sin 19,1 0 = 1,53
Chiếu một tia sáng đơn sắc đến mặt bên của một lăng kính tiết diện là một tam giác đều ABC, theo phưong song song với đáy BC. Tia ló ra khỏi AC đi là là mặt AC. Tính chiết suất của chất làm lăng kính?