cho x/2=y/3=z/5 và x+y+x=-90. Số lớn nhất trong ba số x,y,z là bao nhiêu?

Những câu hỏi liên quan
Cho x 2 = y 3 = z 5 và x + y + z = -90. Số lớn nhất trong ba số x; y; z là
A. 27
B. -27
C. -18
D. -45
Cho
x
2
y
3
z
5
v
à
x
+
y
+
z
-
90
. Số lớn nhất trong ba số x; y; z là? A. 27 B. -27 C. -18 D. -45
Đọc tiếp
Cho x 2 = y 3 = z 5 v à x + y + z = - 90 . Số lớn nhất trong ba số x; y; z là?
A. 27
B. -27
C. -18
D. -45
Ta có: 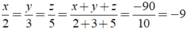
Khi đó ta có: x = -18 ; y = -27 ; z = -45
Số lớn nhất là -18
Chọn đáp án C.
Đúng 0
Bình luận (0)
Cho x 8 = y 7 = z 12 và x + y + z = -108. Số lớn nhất trong ba số x; y; z là
A. 27
B. -27
C. -18
D. -45
1. Cho các số thực x, y, z thỏa mãn điều kiện left{{}begin{matrix}x-y+z3x^2+y^2+z^25end{matrix}right.Pdfrac{x+y-2}{z+2} đạt giá trị lớn nhất là bao nhiêu?2. Cho fleft(xright)2021x^2+dfrac{6y^2}{2021}-4xy-dfrac{y}{2021}+x+dfrac{m^2}{2021}Tìm m để fleft(xright)0forall x,y3. Cho hệ bất phương trình left{{}begin{matrix}left|x+1right|le1dfrac{x}{m} 1end{matrix}right. (m ≠ 0 là tham số thực)Tìm tất cả các giá trị của tham số m để hệ bpt có đúng 3 nghiệm nguyên
Đọc tiếp
1. Cho các số thực x, y, z thỏa mãn điều kiện \(\left\{{}\begin{matrix}x-y+z=3\\x^2+y^2+z^2=5\end{matrix}\right.\)
\(P=\dfrac{x+y-2}{z+2}\) đạt giá trị lớn nhất là bao nhiêu?
2. Cho \(f\left(x\right)=2021x^2+\dfrac{6y^2}{2021}-4xy-\dfrac{y}{2021}+x+\dfrac{m^2}{2021}\)
Tìm m để \(f\left(x\right)>0\forall x,y\)
3. Cho hệ bất phương trình \(\left\{{}\begin{matrix}\left|x+1\right|\le1\\\dfrac{x}{m}< 1\end{matrix}\right.\) (m ≠ 0 là tham số thực)
Tìm tất cả các giá trị của tham số m để hệ bpt có đúng 3 nghiệm nguyên
cho 3 số x,y,z thoả mãn x+y+z >\(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\)và xyz=1
chứng tỏ trong ba số có ít nhất một số lớn hơn 1
Lời giải:
$x+y+z>\frac{1}{x}+\frac{1}{y}+\frac{1}{z}$
$\Leftrightarrow x+y+z>xy+yz+xz$ (do $xyz=1$)
$\Leftrightarrow x+y+z-xy-yz-xz>0$
$\Leftrightarrow xyz+x+y+z-xy-yz-xz-1>0$
$\Leftrightarrow (x-xy)+(y+z-yz-1)+(xyz-xz)>0$
$\Leftrightarrow x(1-y)+(1-y)(z-1)-xz(1-y)>0$
$\Leftrightarrow (1-y)(x+z-1-xz)>0$
$\Leftrightarrow (1-y)(1-z)(x-1)>0$
$\Leftrightarrow (1-y)(1-z)(1-x)<0(*)$
Nếu trong 3 số $x,y,z$ đều nhỏ hơn $1$ thì $(1-y)(1-z)(1-x)>0$ (mâu thuẫn với $(*)$)
Do đó trong 3 số có ít nhất 1 số lớn hơn $1$.
Đúng 1
Bình luận (0)
1. Cho x,y,z là ba số dương thay đổi và thỏa mãn ^{x^2+y^2+z^2le xyz}Hãy tìm giá trị lớn nhất của biểu thức Afrac{x}{x^2+yz}+frac{y}{y^2+zx}+frac{z}{z^2+xy}2. Cho x,y,z là các số thực không âm thỏa mãn x^2+y^2+z^23Tìm giá trị lớn nhất của biểu thức Bxy+yz+zx+frac{5}{x+y+z}
Đọc tiếp
1. Cho x,y,z là ba số dương thay đổi và thỏa mãn \(^{x^2+y^2+z^2\le xyz}\)
Hãy tìm giá trị lớn nhất của biểu thức \(A=\frac{x}{x^2+yz}+\frac{y}{y^2+zx}+\frac{z}{z^2+xy}\)
2. Cho x,y,z là các số thực không âm thỏa mãn \(x^2+y^2+z^2=3\)
Tìm giá trị lớn nhất của biểu thức \(B=xy+yz+zx+\frac{5}{x+y+z}\)
cho 3 số nguyên x y z . Gọi a là tích của x y z . lập câu lệnh viết a thành một lũy thứa bậc n của một số nguyên dương thì số mũ lớn nhất là bao nhiêu trong python
cho 3 số nguyên x y z . Gọi a là tích của x y z . lập câu lệnh viết a thành một lũy thứa bậc n của một số nguyên dương thì số mũ lớn nhất là bao nhiêu trong python
import math
# Nhập 3 số nguyên x, y, z
x = int(input("Nhập số nguyên x: "))
y = int(input("Nhập số nguyên y: "))
z = int(input("Nhập số nguyên z: "))
# Tính tích a của x, y, z
a = x * y * z
# Tìm số mũ lớn nhất n sao cho a có thể viết dưới dạng lũy thừa bậc n của một số nguyên dương
n = int(math.log2(a))
print("Số mũ lớn nhất n mà a có thể viết dưới dạng lũy thừa bậc n của một số nguyên dương là:", n)
Chương trình này sẽ nhận 3 số nguyên từ người dùng, tính tích của chúng, và sau đó tìm số mũ lớn nhất mà tích đó có thể được viết dưới dạng lũy thừa của một số nguyên dương. Chúng tôi sử dụng hàm math.log2 để tính số mũ lớn nhất. Lưu ý rằng kết quả sẽ được làm tròn xuống số nguyên gần nhất.
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất của biểu thức: A = x*y + y*z + z*x
Biết rằng x,y,z là ba số thực và x+y+z=3
Dễ chứng minh được: \(xy\le\frac{x^2+y^2}{2};yz\le\frac{y^2+z^2}{2};zx\le\frac{z^2+x^2}{2}\)
Do đó \(xy+yz+zx\le x^2+y^2+z^2\Leftrightarrow3\left(xy+yz+zx\right)\le x^2+y^2+z^2+2xy+2yz+2zx\)
\(3\left(xy+yz+zx\right)\le\left(x+y+z\right)^2\Leftrightarrow xy+yz+zx\le\frac{\left(x+y+z\right)^2}{3}=3\)
\(\Rightarrow A_{max}=3\Leftrightarrow x=y=z=1\)
Đúng 0
Bình luận (0)














