Tìm giá trị lón nhất của biểu thức sau:Q=9-I10x-4I-6y+24I
Những câu hỏi liên quan
Tìm giá trị lón nhất của biểu thức
a. B=|x- 2006| -|2007- x|
Mk sửa lại đề nha tìm GTNN
a) B=|x- 2006| -|2007- x|
Vì |x- 2006|\(\ge\)0
|2007- x|\(\ge\)0
Suy ra:|x- 2006| -|2007- x|\(\ge\)0
Dấu = xảy ra khi x-2006=0;x=2006
2007-x=0;x=2007
Vậy Min B=0 khi x=2006
x=2007
Đúng 0
Bình luận (1)
\(B=\left|x-2006\right|-\left|2007-x\right|=\left|x-2006\right|-\left|x-2007\right|\)
Áp dụng bđt: \(\left|A\right|-\left|B\right|\le\left|A-B\right|\)
=>\(B\le\left|x-2006-x+2007\right|=1\)
Vậy GTLN của B là 1 khi \(2006\le x\le2007\)
Đúng 0
Bình luận (0)
tìm giá trị lón nhất của biểu thức A= -2x^2-10Y^2+4XY+4X+4Y+2013
giá trị lón nhất của biểu thức B=9x-3x^2
Cho số phức z và w thỏa mãn z+w3+4i và
z
-
w
9
. Tìm giá trị lớn nhất của biểu thức
T
z
+
w
. A. maxT
176
B. maxT14 C. maxT4 D. maxT...
Đọc tiếp
Cho số phức z và w thỏa mãn z+w=3+4i và z - w = 9 .
Tìm giá trị lớn nhất của biểu thức T = z + w .
A. maxT= 176
B. maxT=14
C. maxT=4
D. maxT= 106
Đáp án D
Đặt 
theo giả thiết ta có:
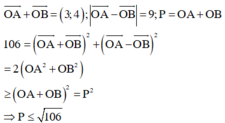
Tổng quát: Với 2 số thực
z
1
,
z
2
thõa mãn 
Khi đó 
Đúng 0
Bình luận (0)
Cho số phức z và w thỏa mãn
z
+
w
3
+
4
i
và
z
-
w
9
Tìm giá trị lớn nhất của biểu thức
T
z
+
w
Đọc tiếp
Cho số phức z và w thỏa mãn z + w = 3 + 4 i và z - w = 9 Tìm giá trị lớn nhất của biểu thức T = z + w
Tìm giá trị nhỏ nhất của biểu thức: P = x² + y² - 2x + 6y + 12
Ta có: \(x^2-2x+y^2+6y+12\)
\(=\left(x^2-2x+1\right)+\left(y^2+6y+9\right)+2\)
\(=\left(x-1\right)^2+\left(y+3\right)^2+2\ge2\forall x,y\)
Dấu '=' xảy ra khi x=1 và y=-3
Đúng 1
Bình luận (0)
1 Tìm GTNN của biểu thức
a,A=I2x-4I+3-2x
b,B=Ix+1I+Ix+2I+Ix+3I+x+4I
2 Tìm giá trị lớn nhất của biểu thức
A=Ix-2I-Ix-7I
1 Tìm GTNN của biểu thức
a,A=I2x-4I+3-2x
b,B=Ix+1I+Ix+2I+Ix+3I+x+4I
2 Tìm giá trị lớn nhất của biểu thức
A=Ix-2I-Ix-7I
1 Tìm GTNN của biểu thức
a,A=I2x-4I+3-2x
b,B=Ix+1I+Ix+2I+Ix+3I+x+4I
2 Tìm giá trị lớn nhất của biểu thức
A=Ix-2I-Ix-7I