Cho tam giác ABC vẽ tam giác A’B’C’ đồng dạng với tam giác ABC theo tỉ số đồng dạng là K = 2/3.

Những câu hỏi liên quan
Biết tam giác ABC đồng dạng với tam giác A’B’C’ theo tỉ số đồng dạng k = 4/5 . Khi đó tam giác A’B’C’ đồng dạng với tam giác ABC theo tỉ số đồng dạng là:
A. 5 4
B. 4 5
C. 1 5
D. 3 4
Cho tam giác ABC và tam giác A’B’C’ đồng dạng với nhau theo tỉ số k. a,Tìm tỉ số 2 đường cao tương ứng AH/A’H’ theo k b,Tìm tỉ số diện tích của tam giác ABC và tam giác A’B’C’ theo k
b) Ta có: ΔABC\(\sim\)ΔA'B'C'(gt)
nên \(\dfrac{S_{ABC}}{S_{A'B'C'}}=\left(\dfrac{AB}{A'B'}\right)^2\)(Định lí tỉ số diện tích của hai tam giác đồng dạng)
hay \(\dfrac{S_{ABC}}{S_{A'B'C'}}=k^2\)
Đúng 1
Bình luận (0)
Cho tam giác ABC đồng dạng với tam giác A’B’C’ tỉ số đồng dạng là 1/2 biết AB=3cm AC=4cm BC=5cm
a) tính các cạnh của tam giác A’B’C’
b) vẽ MN song song với B’C’ . Chứng minh tam giác ABC đồng dạng với tam giác A’MN
c) Biết A’M=4cm. Tính A’M; MN
d) kẻ A’H vuông góc với B’C’; A’H cắt MN tại K. Tính A’H và A’K
a: ΔABC~ΔA'B'C'
=>\(\frac{AB}{A^{\prime}B^{\prime}}=\frac{AC}{A^{\prime}C^{\prime}}=\frac{BC}{B^{\prime}C\text{'}}=\frac12\)
=>\(\frac{3}{A^{\prime}B^{\prime}}=\frac{4}{A^{\prime}C^{\prime}}=\frac{5}{B^{\prime}C^{\prime}}=\frac12\)
=>\(A^{\prime}B^{\prime}=3\cdot2=6\left(\operatorname{cm}\right);A^{\prime}C^{\prime}=4\cdot2=8\left(\operatorname{cm}\right);B^{\prime}C^{\prime}=5\cdot2=10\left(\operatorname{cm}\right)\)
b: Xét ΔA'B'C' có MN//B'C'
nên ΔA'MN~ΔA'B'C'
=>\(\hat{A^{\prime}MN}=\hat{A^{\prime}B^{\prime}C^{\prime}}\) (1) và \(\hat{A^{\prime}NM}=\hat{A^{\prime}C^{\prime}B^{\prime}}\) (2)
ΔABC~ΔA'B'C'
=>\(\hat{ABC}=\hat{A^{\prime}B^{\prime}C^{\prime}}\left(3\right);\hat{ACB}=\hat{A^{\prime}C^{\prime}B^{\prime}}\left(4\right)\)
Từ (1),(3) suy ra \(\hat{A^{\prime}MN}=\hat{ABC}\)
Từ (2),(4) suy ra \(\hat{A^{\prime}NM}=\hat{ACB}\)
Xét ΔA'MN và ΔABC có
\(\hat{A^{\prime}MN}=\hat{ABC}\)
\(\hat{A^{\prime}NM}=\hat{ACB}\)
Do đó: ΔA'MN~ΔABC
c: Xét ΔA'B'C' có MN//B'C'
nên \(\frac{MN}{B^{\prime}C^{\prime}}=\frac{A^{\prime}M}{AB}\)
=>\(\frac46=\frac{MN}{10}\)
=>\(MN=10\cdot\frac46=\frac{40}{6}=\frac{20}{3}\) (cm)
Đúng 0
Bình luận (0)
Cho tam giác A’B’C’ có A’E’ là đường phân giác và tam giác ABC có AE là đường phân giác.Biết tam giác A’B’C’ ~ tam giác ABC theo tỉ số đồng dạng k. CM A’E’/ AE=k
ΔA'B'C' đồng dạng với ΔABC
=>A'B'/AB=B'C'/BC=A'C'/AC=k và góc A'=góc A; góc B=góc B' góc C'=góc C
=>góc BAE=góc B'A'E'
Xét ΔABE và ΔA'B'E' có
góc B=góc B'
góc BAE=góc B'A'E'
=>ΔABE đồng dạng với ΔA'B'E'
=>AE/A'E'=AB/A'B'
=>A'E'/AE=A'B'/AB=k
Đúng 0
Bình luận (0)
Cho tam giác ABC, vẽ tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số đồng dạng k = 2/3.
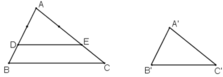
+ Dựng ΔADE 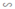 ΔABC theo tỉ số 2/3
ΔABC theo tỉ số 2/3
Trên AB lấy D, trên AC lấy E sao cho 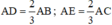
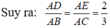
Khi đó theo định lý Ta-let đảo ta suy ra DE // BC
⇒ ΔADE 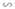 ΔABC theo tỉ số 2/3.
ΔABC theo tỉ số 2/3.
+ Dựng ΔA’B’C’ = ΔADE
Vẽ đoạn A’B’ = AD.
Dựng góc 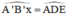
Trên tia B’x lấy điểm C’ sao cho B’C’ = DE.
Nối C’A’ ta được ΔA’B’C’ = ΔADE (c.g.c)
Suy ra: ΔA’B’C’ đồng dạng với ΔADE theo tỉ số:
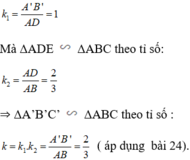
Đúng 0
Bình luận (0)
Cho ABC có AB=6cm; AC=8cm, BC=12cm. Tam giác A’B’C’ đồng dạng với tam giác ABC với tỉ số đồng dạng là 3/2.
a) Tính độ dài các cạnh của tam giác A’B’C’
b) Tính tỉ số chu vi của hai tam giác trên
a: Ta có: ΔA'B'C'∼ΔABC
nên A'B'/AB=B'C'/BC=A'C'/AC
=>A'B'/6=B'C'/12=A'C'/8=3/2
=>A'B'=9cm; B'C'=18cm; A'C'=12cm
b: Ta có: ΔA'B'C'∼ΔABC
nên \(\dfrac{C_{A'B'C'}}{C_{ABC}}=\dfrac{3}{2}\)
Đúng 0
Bình luận (0)
Hãy chọn câu trả lời đúng. Nếu tam giác ABC đồng dạng với tam giác A’B’C’ theo tỉ số k thì tỉ số chu vi của tam giác A’B’C’ và ABC bằng
A. 1
B. 1 k
C. k
D. k 2
Vì tam giác ABC đồng dạng với tam giác A’B’C’ theo tỉ số k nên A B A ' B ' = A C A ' C ' = B C B ' C ' = k
Suy ra A ' B ' A B = A ' C ' A C = B ' C ' B C = 1 k
Áp dụng tính chất dãy tỉ số bằng nhau ta có
A ' B ' A B = A ' C ' A C = B ' C ' B C = A ' B ' + A ' C ' + B ' C ' A B + A C + B C = 1 k
Vậy tỉ số chu vi của tam giác A’B’C’ và ABC là 1 k
Đáp án: B
Đúng 0
Bình luận (0)
cho tam giác abc đồng dạng với tam giác khg theo tỉ số 2:3 và tam giác khg đồng dạng với tam giác mnp theo tỉ số 1:3 vậy tam giác abc đồng dạng với tam giác mnp theo tỉ số nào
a)k=3:9. b) k=2:9. c) k=2:6 d) k=1:3
Cho tam giác \(ABC\), hãy vẽ một tam giác đồng dạng với tam giác \(ABC\) theo tỉ số đồng dạng \(k = \frac{1}{2}\).
Bước 1: Vẽ tam giác \(ABC\) bất kì.
Bước 2: Gọi \(M\) là trung điểm của \(AB\), \(N\) là trung điểm của \(AC\).
Khi đó ta có \(\Delta AMN\backsim\Delta ABC\) theo tỉ số \(k = \frac{1}{2}\).
Chứng minh:
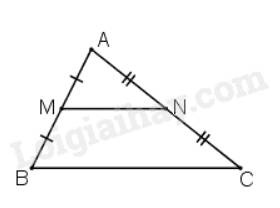
Vì \(M\) là trung điểm của \(AB\), \(N\) là trung điểm của \(AC\) nên \(MN\) là đường trung bình của tam giác \(ABC\)\( \Rightarrow \left\{ \begin{array}{l}MN//BC\\MN = \frac{1}{2}BC\end{array} \right.\).
Ta có \(MN//BC\) và \(M,N\) cắt \(AB,AC\) tại \(M,N\) nên \(\Delta AMN\backsim\Delta ABC\) (định lí).
Khi đó, \(\frac{{MN}}{{BC}} = \frac{1}{2}\)
Đúng 0
Bình luận (0)














