giải phương trình nghiệm nguyên: 5x2+2xy+y2-4x-40 bằng 0
tìm nghiệm nguyên của phương trình 2xy + 4x + 2y + 1 > 5x2 + 2y2
\(\Leftrightarrow\left(x^2-2xy+y^2\right)+\left(4x^2-4x+1\right)+\left(y^2-2y+1\right)< 3\)
\(\Leftrightarrow\left(x-y\right)^2+\left(2x-1\right)^2+\left(y-1\right)^2< 3\)
\(\Rightarrow\left(2x-1\right)^2< 3\) (1)
\(\Rightarrow\left(2x-1\right)^2=\left\{0;1\right\}\)
\(\Rightarrow\left[{}\begin{matrix}2x-1=0\\2x-1=1\\2x-1=-1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
- Với \(x=0\Rightarrow2y^2-2y< 1\Rightarrow\left(2y-1\right)^2< 3\Rightarrow\left[{}\begin{matrix}y=0\\y=1\end{matrix}\right.\) (giải như (1))
- Với \(x=1\Rightarrow2y^2+5< 4y+5\Rightarrow y^2-2y< 0\)
\(\Rightarrow y\left(y-2\right)< 0\Rightarrow0< y< 2\Rightarrow y=1\)
Vậy \(\left(x;y\right)=\left(0;0\right);\left(0;1\right);\left(1;1\right)\)
Tìm nghiệm nguyên của phương trình 2xy + 4x + 2y + 1 > 5x2 + 2y2 . Giúp mình với ạ. Mình cần gấp
Giải phương trình 5 x 2 + 4 x – 1 = 0 bằng cách điền vào những chỗ trống:
a = …; b’ = …; c = …;
Δ’ = …; √(Δ') = ….
Nghiệm của phương trình:
x 1 = … ; x 2 = … .
a = 5; b’ = 2; c = -1;
Δ ’ = ( b ' ) 2 - a c = 2 2 - 5 . ( - 1 ) = 9 ; √(Δ') = 3
Nghiệm của phương trình:
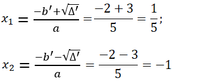
Giải phương trình 5x2 + 4x – 1 = 0 bằng cách điền vào những chỗ trống:
a = …; b’ = …; c = …;
Δ’ = …; √(Δ') = ….
Nghiệm của phương trình:
x1 = …; x2 = ….
a = 5; b’ = 2; c = -1;
Δ’ = (b')2 - ac = 22 - 5.(-1) = 9; √(Δ') = 3
Nghiệm của phương trình:
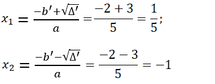
Giải phương trình nghiệm nguyên:\(x^2+2y^2-2xy+4x-3y-26=0\)
Hệ phương trình 2 x y + y 2 − 4 x − 3 y + 2 = 0 x y + 3 y 2 − 2 x − 14 y + 16 = 0 có nghiệm là:
A. x ∈ R , y = 2 ; x = − 1 , y = 3
B. x = 3 , y = − 1 ; x = 2 , y = − 1 2
C. x = 5 , y = 2 ; x = 1 , y = 3 ; x = 1 2 , y = 2
D. x ∈ R , y = 2 ; x = 1 , y = 3
Ta có: 2 x y + y 2 − 4 x − 3 y + 2 = 0 x y + 3 y 2 − 2 x − 14 y + 16 = 0 ⇒ 2 x y + y 2 − 4 x − 3 y + 2 = 0 2 x y + 6 y 2 − 4 x − 28 y + 32 = 0
⇒ 5 y 2 − 25 y + 30 = 0 ⇒ y = 3 ; y = 2
Khi y = 3 thì phương trình đầu trở thành 6 x + 9 - 4 x - 9 + 2 = 0 ⇔ x = - 1
Khi y = 2 thì phương trình đầu trở thành 4 x + 4 - 4 x - 6 + 2 = 0
⇔ 0 x = 0 ⇔ x ∈ R
Đáp án cần chọn là: A
giải phương trình nghiệm nguyên sau: 2xy-4x-y=1
\(2xy-4x-y=1\Rightarrow2xy-4x-y+2=3\Rightarrow2x\left(y-2\right)-\left(y-2\right)=3\Rightarrow\left(2x-1\right)\left(y-2\right)=3\)
Vì x,y là nghiệm nguyên nên ta xét các trường hợp :
1. \(\hept{\begin{cases}2x-1=1\\y-2=3\end{cases}\Leftrightarrow\hept{\begin{cases}x=1\\y=5\end{cases}}}\)
2. \(\hept{\begin{cases}2x-1=3\\y-2=1\end{cases}\Leftrightarrow}\hept{\begin{cases}x=2\\y=3\end{cases}}\)
3. \(\hept{\begin{cases}2x-1=-1\\y-2=-3\end{cases}\Leftrightarrow\hept{\begin{cases}x=0\\y=-1\end{cases}}}\)
4. \(\hept{\begin{cases}2x-1=-3\\y-2=-1\end{cases}\Leftrightarrow}\hept{\begin{cases}x=-1\\y=1\end{cases}}\)
Vậy nghiệm của phương trình là : \(\left(x;y\right)=\left(-1;1\right);\left(0;-1\right);\left(1;5\right);\left(2;3\right)\)
2xy-4x-y=1
x(2y-4)-y=1
2x(2y-4)-2y=2
2x(2y-4)-2y+4=6
2x(2y-4)-(2y-4)=6
(2y-4)(2x-1)=6
Đến đây, ta thấy 2x-1 là ước lẻ của 6 =>2x-1 E { 1;3 }
Với 2x-1=1 thì 2y-4=6 =>x=1, y=5
Với 2x-1=3 thì 2y-4=2 =>x=2, y=3
Em mới học lớp 6 nên chỉ làm theo cách lớp 6 thôi. Còn nghiệm nguyên thì em chưa học
2xy-4x-y=1
x(2y-4)-y=1
2x(2y-4)-2y=2
2x(2y-4)-2y+4=6
2x(2y-4)-(2y-4)=6
(2y-4)(2x-1)=6
Đến đây, ta thấy 2x-1 là ước lẻ của 6 =>2x-1 E { 1;3 }
Với 2x-1=1 thì 2y-4=6 =>x=1, y=5
Với 2x-1=3 thì 2y-4=2 =>x=2, y=3
Tìm nghiệm nguyên của phương trình 2xy-4x+y-9=0
\(2xy-4x+y-9=0\)
\(\Leftrightarrow2x\left(y-2\right)+\left(y-2\right)-7=0\)
\(\Leftrightarrow\left(2x+1\right)\left(y-2\right)=7\)
\(\Rightarrow2x+1\) và \(y-2\) là ước của 7
đến đây dễ rồi tự làm nha
x=0 và y=9 ; x=3 và y=3
x=-1 và y=-5 ; x=-4 và y=1
đúng ko nhỉ
Áp dụng công thức nghiệm để giải các phương trình:
a ) 5 x 2 − x + 2 = 0 b ) 4 x 2 − 4 x + 1 = 0 c ) − 3 x 2 + x + 5 = 0
a) 5 x 2 – x + 2 = 0 ;
a = 5; b = -1; c = 2
Δ = b 2 - 4 a c = ( - 1 ) 2 - 4 . 5 . 2
= 1 - 40 = -39 < 0
Vậy phương trình trên vô nghiệm.
b) 4 x 2 – 4 x + 1 = 0 ;
a = 4; b = -4; c = 1
Δ = b 2 - 4 a c = ( - 4 ) 2 - 4 . 4 . 1 = 16 - 16 = 0
⇒ phương trình có nghiệm kép
x = (-b)/2a = (-(-4))/2.4 = 1/2
Vậy phương trình có nghiệm duy nhất x = 1/2
c) - 3 x 2 + x + 5 = 0
a = -3; b = 1; c = 5
Δ = b 2 - 4 a c = 12 - 4 . ( - 3 ) . 5 = 1 + 60 = 61 > 0
⇒ Do Δ >0 nên áp dụng công thức nghiệm, phương trình có 2 nghiệm phân biệt
x 1 = ( 1 - √ 61 ) / 6 ; x 2 = ( 1 + √ 61 ) / 6