Cho 3 hình tròn có bán kính lần lượt là R1,R2,R3 , có diện tích lần lượt là S1,S2,S3 tiếp xúc ngoài và cùng tiếp xúc với đường thẳng d, trong đó R3 là bán kính nhỏ nhất. tìm gtnn của \(\sqrt{S_1S_2}\) theo R3.
Những câu hỏi liên quan
Cho 3 hình tròn có bán kính r1, r2, r3 và có diện tích lần lượt là S1,S2,S3 tiếp xúc ngoài với nhau và cùng tiếp xúc với đường thẳng (d). Trong đó r3 nhỏ nhất. Tìm min căn(S1×S2) theo độ dài cho trước r3.
Cho tứ diện đều ABCD có mặt cẩu nội tiếp là (S1) và mặt cầu ngoại tiếp là (S2). Một hình lập phương ngoại tiếp (S2) và nội tiếp trong mặt cầu (S3). Gọi
r
1
,
r
2
,
r
3
lần lượt là bán kính các mặt cầu (S1), (S2), (S3). Khẳng định nào sau đây là đúng A.
r
1
r
2...
Đọc tiếp
Cho tứ diện đều ABCD có mặt cẩu nội tiếp là (S1) và mặt cầu ngoại tiếp là (S2). Một hình lập phương ngoại tiếp (S2) và nội tiếp trong mặt cầu (S3). Gọi r 1 , r 2 , r 3 lần lượt là bán kính các mặt cầu (S1), (S2), (S3). Khẳng định nào sau đây là đúng
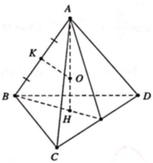
A. r 1 r 2 = 2 3 và r 2 r 3 = 1 3
B. r 1 r 2 = 2 3 và r 2 r 3 = 1 2
C. r 1 r 2 = 1 3 và r 2 r 3 = 1 3
D. r 1 r 2 = 1 3 và r 2 r 3 = 1 3 3
Cho tứ diện đều ABCD có mặt cầu nội tiếp là
S
1
và mặt cầu ngoại tiếp là
S
2
. Một hình lập phương ngoại tiếp
S
2
và nội tiếp trong mặt cầu
S
2
. Gọi
r
1
,
r
2
,
...
Đọc tiếp
Cho tứ diện đều ABCD có mặt cầu nội tiếp là S 1 và mặt cầu ngoại tiếp là S 2 . Một hình lập phương ngoại tiếp S 2 và nội tiếp trong mặt cầu S 2 . Gọi r 1 , r 2 , r 3 lần lượt là bán kính các mặt cầu S 1 , S 2 , S 3 . Khẳng định nào sau đây đúng?
Cho tứ diện đều ABCD có mặt cầu nội tiếp là
S
1
và mặt cầu ngoại tiếp là
S
2
. Một hình lập phương ngoại tiếp
S
2
và nội tiếp trong mặt cầu
S
2
. Gọi
r
1
,
r
2...
Đọc tiếp
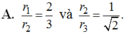
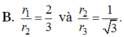
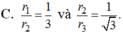
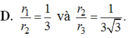
Cho tứ diện đều ABCD có mặt cầu nội tiếp là S 1 và mặt cầu ngoại tiếp là S 2 . Một hình lập phương ngoại tiếp S 2 và nội tiếp trong mặt cầu S 2 . Gọi r 1 , r 2 , r 3 lần lượt là bán kính các mặt cầu ( S 1 ) , ( S 2 ) , ( S 3 ) . Khẳng định nào sau đây đúng?
A. r 1 r 2 = 2 3 và r 2 r 3 = 1 2 .
B. r 1 r 2 = 2 3 và r 2 r 3 = 1 3 .
C. r 1 r 2 = 1 3 và r 2 r 3 = 1 3 .
D. r 1 r 2 = 1 3 và r 2 r 3 = 1 3 3 .
Trong không gian Oxyz, cho mặt cầu (S1) có tâm I1(2;1;0), bán kính R1 3; mặt cầu (S2) có tâm I2(0;1;0), bán kính R2 2. Đường thẳng d thay đổi nhưng luôn tiếp xúc với cả hai mặt cầu (S1),(S2). Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của khoảng cách từ điểm A(1;1;1) đến đường thẳng d. Giá trị của M.m bằng A.5,5 B. 4,5 C. 6,5 D. 7,5
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S1) có tâm I1(2;1;0), bán kính R1 = 3; mặt cầu (S2) có tâm I2(0;1;0), bán kính R2 = 2. Đường thẳng d thay đổi nhưng luôn tiếp xúc với cả hai mặt cầu (S1),(S2). Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của khoảng cách từ điểm A(1;1;1) đến đường thẳng d. Giá trị của M.m bằng
A.5,5
B. 4,5
C. 6,5
D. 7,5
Trong không gian với hệ toạ độ Oxyz, cho bốn điểm A(1;1;1),B(-2;1;-3),C(4;1;-3),D(1;
1
+
2
3
;-1). Gọi
(
S
1
)
,
(
S
2
)
,
(
S
3
)
,
(
S
4
)
lần lượt là các mặt cầu tâm A,B,C,D và có bán kính tương ứng là 2;3;3;2....
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho bốn điểm A(1;1;1),B(-2;1;-3),C(4;1;-3),D(1; 1 + 2 3 ;-1). Gọi ( S 1 ) , ( S 2 ) , ( S 3 ) , ( S 4 ) lần lượt là các mặt cầu tâm A,B,C,D và có bán kính tương ứng là 2;3;3;2. Mặt cầu tiếp xúc ngoài với cả 4 mặt cầu ( S 1 ) , ( S 2 ) , ( S 3 ) , ( S 4 ) có bán kính bằng
A. 5 9
B. 3 7
C. 7 15
D. 6 11
Trong không gian Oxyz, cho ba điểm A(-1;3;-1), B(-2;1;1), C(0;1;1). Gọi (S1), (S2), (S3) là các mặt cầu đôi một tiếp xúc ngoài với nhau và tiếp xúc với mặt phẳng (ABC) lần lượt tại A, B và C. Tích bán kính của ba mặt cầu (S1), (S2), (S3) bằng A.
9
4
B. 9 C. 18 D. 36
Đọc tiếp
Trong không gian Oxyz, cho ba điểm A(-1;3;-1), B(-2;1;1), C(0;1;1). Gọi (S1), (S2), (S3) là các mặt cầu đôi một tiếp xúc ngoài với nhau và tiếp xúc với mặt phẳng (ABC) lần lượt tại A, B và C. Tích bán kính của ba mặt cầu (S1), (S2), (S3) bằng
A. 9 4
B. 9
C. 18
D. 36
Gọi O1, O2, O3 lần lượt là tâm của ba mặt cầu đã cho và bán kính tương ứng là x, y,z ta có điều kiện các mặt cầu đôi một tiếp xúc ngoài là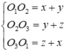 
và điều kiện tiếp xúc với mặt phẳng
(ABC) là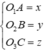 
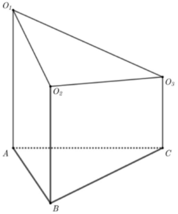
Vậy theo pitago có
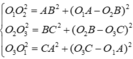
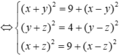
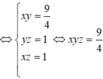
Chọn đáp án A.
Đúng 0
Bình luận (0)
Cho một hình lập phương có bán kính mặt cầu ngoại tiếp, mặt cầu nội tiếp và mặt cầu tiếp xúc với tất cả các cạnh của hình lập phương lần lượt là
R
1
,
R
2
,
R
3
. Mệnh đề nào sau đây đúng? A.
R
1
R
3
R
2
B. ...
Đọc tiếp
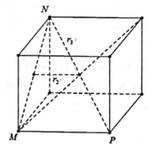
Cho một hình lập phương có bán kính mặt cầu ngoại tiếp, mặt cầu nội tiếp và mặt cầu tiếp xúc với tất cả các cạnh của hình lập phương lần lượt là R 1 , R 2 , R 3 . Mệnh đề nào sau đây đúng?
A. R 1 > R 3 > R 2
B. R 1 > R 2 > R 3
C. R 3 > R 1 > R 2
D. R 2 > R 1 > R 3
Đáp án A
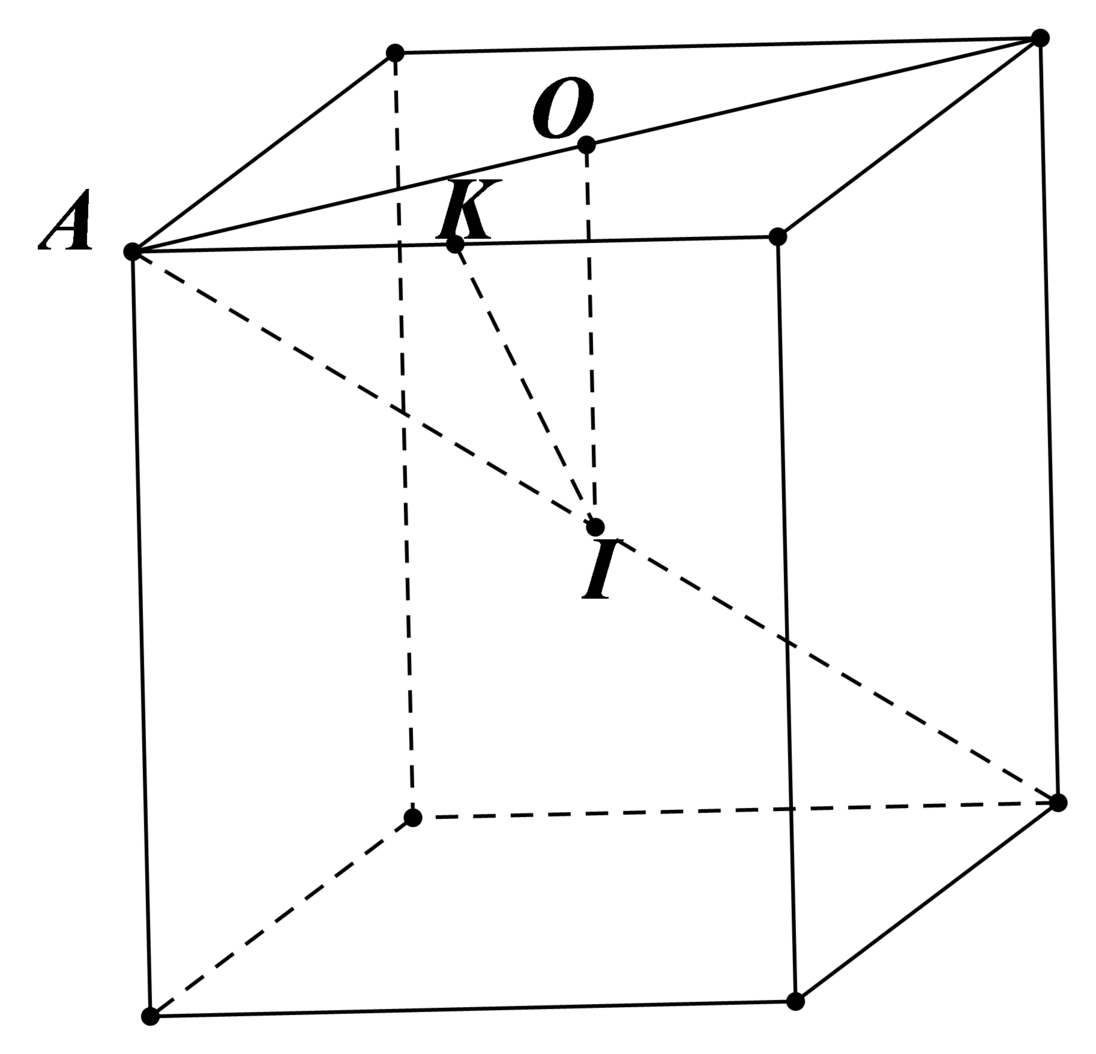
Ta có: R 1 = I A , R 2 = I O , R 3 = I K . Mà I A > I K > I O nên R 1 > R 3 > R 2 .
Đúng 0
Bình luận (0)
Cho một hình lập phương có bán kính mặt cầu ngoại tiếp, mặt cầu nội tiếp và mặt cầu tiếp xúc với tất cả các cạnh của hình lập phương lần lượt là
R
1
,
R
2
,
R
3
. Mệnh đề nào sau đây đúng?
Đọc tiếp
Cho một hình lập phương có bán kính mặt cầu ngoại tiếp, mặt cầu nội tiếp và mặt cầu tiếp xúc với tất cả các cạnh của hình lập phương lần lượt là R 1 , R 2 , R 3 . Mệnh đề nào sau đây đúng?
