cho đường tròn tâm O đường kính AB = 2R. trên nửa đường tròn đường kính AB lấy C và D sao cho góc COD = 90 độ, AC cắt BD tại M.
a, chứng ming tam giác MCO đồng dạng với tam giác MBA. tính tỉ số đồng dạng
b, cho góc CBA = 30 độ. tính cung BC nhỏ
Cho nửa đường tròn (O; R) đường kính AB. Vẽ dây CD = R (thuộc cung AD). Nối AC và BD cắt nhau tại M
a, Chứng minh tam giác MCD đồng dạng với tam giác MBA. Tìm tỉ số đồng dạng
b, Cho A B C ^ = 30 0 , tính độ dài cung nhỏ AC
a, Khi M ở ngoài hay M nằm trong đường tròn thì ∆MCD và ∆MBA đều có 2 góc bằng nhau => ĐPCM
Tỷ số đồng dạng là: C D A B = 1 2
b, A B C ^ = 30 0 => A O C ^ = 60 0 => l A C ⏜ = πR 3
Cho nửa đường tròn (O; R) đường kính AB. Kẻ Ax và By là hai tiếp tuyến của nửa đường tròn tại A và B. Trên Ax lấy điểm C bất kì, đường thẳng qua O và vuông góc với OC cắt By tại D. a) Chứng minh AC. BD = R2 . b) Chứng minh tam giác COD đồng dạng với tam giác ODB. c) Chứng minh CD là tiếp tuyến của (O). e) Tìm vị trí của điểm C trên Ax để tứ giác ACDB có chu vi nhỏ nhất.
Cho nửa đường tròn tâm O, đường kính AB = 2R, Ax và By là hai tiêp tuyến với nửa đường tròn tại A và B. Lấy trên tia Ax điểm M rồi vẽ tiếp tuyến MP với đường tròn tâm O (tiếp điểm P khác điểm A) cắt By tại N
a, Chứng minh các tam giác MON và APB đồng dạng
b, Chứng minh AM.BN = R 2
c, Tính tỉ số S M O N S A P B khi AM = R 2
d, Tính thể tích của hình do nửa hình tròn đường kính AB quay một vòng quanh AB sinh ra
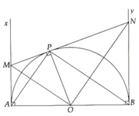
a, Sử dụng các tứ giác nội tiếp chứng minh được P M O ^ = P A O ^ và P N O ^ = P B O ^ => ∆MON và ∆APB đồng dạng (g.g)
b, Theo tính chất hai tiếp tuyến cắt nhau ta có: MP = MA và NP = NB
Mặt khác MP.NP = P O 2 và PO = R Þ AM.BN = R 2 (ĐPCM)
c, Ta có A M = R 2 => M P = R 2
Mặt khác A M = R 2 => BN = 2R => PN = 2R
Từ đó tìm được MN = 5 R 2
Vì DMON và DAPB đồng dạng nên S M O N S A P B = M N A B 2 = 25 16
d, Khi quay nửa đường tròn đường kính AB xung quanh AB ta được hình cầu với tâm O và bán kính R' = OA = R
Thể tích hình cầu đó là V = 4 3 πR 3 (đvdt)
Cho nửa đường tròn tâm O đường kính AB=2R. Trên cùng một nửa mặt phẳng bờ AB có chứa nửa đường tròn kẻ các tia tiếp tuyến Ax,By của đường tròn.Trên Ax,By lấy C,D sao cho CD=AC+BD. CMR: a,COD = 90* b, AB tiếp xúc với đường trong ngoại tiếp tam giác COD
Cho nửa đường tròn (O) đường kính AB. Lấy M là điểm tuỳ ý trên nửa đường tròn (M khác A và B). Kẻ MH vuông góc với AB (H ∈ AB). Trên cùng nửa mặt phang bờ AB chứa nửa đường tròn (O) vẽ hai nửa đường tròn tâm O 1 , đường kính AH và tâm O 2 , đường kính BH. Đoạn MA và MB cắt hai nửa đường tròn ( O 1 ) và ( O 2 ) lần lượt tại P và Q. Chứng minh:
a, MH = PQ
b, Các tam giác MPQ và MBA đồng dạng
c, PQ là tiếp tuyến chung của hai đường tròn ( O 1 ) và ( O 2 )
a, MPHQ là hình chữ nhật => MH = PQ
b, Sử dụng hệ thức lượng trong tam giác vuông chứng minh được MP.MA = MQ.MB => ∆MPQ: ∆MBA
c, P M H ^ = M B H ^ => P Q H ^ = O 2 Q B ^ => PQ là tiếp tuyến của O 2
Tương tự PQ cũng là tiếp tuyến ( O 1 )
Cho nửa đường tròn tâm O đường kính AB=2R. Trên nửa đường tròn lấy điểm M sao cho MB=R.
Tiếp tuyến tại M của đường tròn cắt các tiếp tuyến Ax, By lần lượt tại C và D (Ax và By cùng thuộc một
nửa mặt phẳng có bờ AB chứa điểm M)
a) Chứng minh tam giác COD vuông và AC+BD=CD
b) Tính OC theo R?
c) BC cắt đường tròn tại F (F khác B). Đường thẳng qua O vuông góc với BC cắt By tại E. Chứng minh
EF là tiếp tuyến của đường tròn (O).
d) Gọi K là giao điểm của OE và BC. Chứng minh DM=DK.
a: Xét (O) có
CM là tiếp tuyến có M là tiếp điểm
CA là tiếp tuyến có A là tiếp điểm
Do đó: OC là tia phân giác của \(\widehat{AOM}\)
Xét (O) có
DM là tiếp tuyến có M là tiếp điểm
DB là tiếp tuyến có B là tiếp điểm
Do đó: OD là tia phân giác của \(\widehat{BOM}\)
Ta có: \(\widehat{AOM}+\widehat{BOM}=180^0\)
\(\Leftrightarrow2\cdot\left(\widehat{MOC}+\widehat{MOD}\right)=180^0\)
hay \(\widehat{COD}=90^0\)
Cho nửa đường tròn tâm O đường kính AB=2R. Trên nửa đường tròn lấy điểm M sao cho MB=R.
Tiếp tuyến tại M của đường tròn cắt các tiếp tuyến Ax, By lần lượt tại C và D (Ax và By cùng thuộc một
nửa mặt phẳng có bờ AB chứa điểm M)
a) Chứng minh tam giác COD vuông và AC+BD=CD
b) Tính OC theo R?
c) BC cắt đường tròn tại F (F khác B). Đường thẳng qua O vuông góc với BC cắt By tại E. Chứng minh
EF là tiếp tuyến của đường tròn (O).
d) Gọi K là giao điểm của OE và BC. Chứng minh DM=DK.
a: Xét (O) có
CM là tiếp tuyến có M là tiếp điểm
CA là tiếp tuyến có A là tiếp điểm
Do đó: CM=CA
Xét (O) có
DM là tiếp tuyến có M là tiếp điểm
DB là tiếp tuyến có B là tiếp điểm
Do đó: DM=DB
Ta có: MC+MD=CD
mà MC=CA
và MD=DB
nên CD=AC+BD
1 .
Cho nửa đường tròn tâm O ,đường kính AB = 2R .M là một điểm tùy ý trên đường tròn (M≠A,B) .Kẻ hai tiếp tuyến Ax ,By với nửa đường tròn (Ax ,By và nửa đường đường tròn cùng nằm trên một mặt phẳng bờ AB).Qua M kẻ tiếp tuyến thứ 3 với đường tròn cắt Ax và By tại C và D
a. C/M : CD = AC + BD và tam giác COD vuông tại O
b.Chứng minh:AC.BD=R2
c.Cho biết AM=R.Tính theo R diện tích △BDM.
d.AD cắt BC tại N.Chứng minh MN // Ac
2 .
Cho hình chữ nhật ABCD có AB=12cm ,BC=9cm.Gọi H là chân đường vuông góc kẻ từ A đến BD
a,Chứng minh: tam giác AHB đồng dạng với tam giác BCD
b,tính độ dài đoạn AH
c, Chứng minh AH.AH=BH.DH
Bài 2 :
a ) Ta có : \(AH\perp BD\Rightarrow\widehat{AHD}=\widehat{BCD}=90^0\)
AD//BC \(\Rightarrow\widehat{ADH}=\widehat{DBC}\)
\(\Rightarrow\Delta AHB~\Delta DCB\left(g.g\right)\)
b ) Ta có : \(AB=12,BC=9\Rightarrow BD=\sqrt{AB^2+BC^2}=15\)
Từ câu a \(\Rightarrow\frac{AH}{CD}=\frac{AB}{DB}\)
\(\Rightarrow AH=\frac{AB.CD}{DB}=\frac{12.12}{15}=\frac{48}{5}\)
c ) Ta có \(\widehat{DAH}=\widehat{ABH}\left(+\widehat{BAH}=90^0\right)\)
\(\widehat{AHB}=\widehat{AHD}=90^0\)
\(\Rightarrow\Delta ADH~\Delta BAH\left(g.g\right)\)
\(\Rightarrow\frac{AH}{BH}=\frac{DH}{AH}\Rightarrow AH.AH=BH.DH\)
Cho nửa đường tròn tâm O, đường kính AB = 2R, Ax và By là hai tiếp tuyến với nửa đường tròn tại A và B. Lấy trên tia Ax điểm M rồi vẽ tiếp tuyến MP cắt By tại N.
a, Chứng minh MON và APB là hai tam giác vuông đồng dạng
b, Chứng minh AM.BN = R 2
c, Tính tỉ số S M O N S A P B khi AM = R 2
d, Tính thể tích của hình do nửa hình tròn APB quay quanh AB sinh ra
a), b) HS tự chứng minh
c, AM = R 2 => S M O N S A P B = 25 16
d, V = 4 3 πR 3