Cho ∆ABC có góc B = 60°, góc C =45°. Vẽ (O) ngoại tiếp ∆ABC. Tính số đo các cung BC

Những câu hỏi liên quan
Bài 1: Cho nửa đường tròn (O) đường kính AB và dây cung AC. N là điểm chính giữa của cung CB. Chưng minh AN là tia phân giác của góc CABBài 2: Cho tam giác ABC nhọn nối tiếp đường trnf (O) đường kính BD. Biết góc BAC bằng 45 độ. Tính số đo góc CBD Bài 3 cho tam giác ABC nhọn có góc BAC 60 độ. vẽ đường tròn đường kính BC tâm O cắt AB, AC lần lượt tại D và E. tính số đo góc ODEgiúp mình với mình đang cần gấp :((
Đọc tiếp
Bài 1: Cho nửa đường tròn (O) đường kính AB và dây cung AC. N là điểm chính giữa của cung CB. Chưng minh AN là tia phân giác của góc CAB
Bài 2: Cho tam giác ABC nhọn nối tiếp đường trnf (O) đường kính BD. Biết góc BAC bằng 45 độ. Tính số đo góc CBD
Bài 3 cho tam giác ABC nhọn có góc BAC= 60 độ. vẽ đường tròn đường kính BC tâm O cắt AB, AC lần lượt tại D và E. tính số đo góc ODE
giúp mình với mình đang cần gấp :((
Cho tam giác ABC có B 70° ; C 50° nội tiếp trong đường tròn ( O ) .
a ) Tính số đo cung BC .
b ) Gọi AD , BE , CF lần lượt là các đường phân giác của các góc A , B , C . Tính : • Số đo các góc BEC , BED và FDE . • Số đo các cung CBF ; BCE . .
c ) Cho BC 6 cm . Tính bán kính đường tròn ( O ) .
Đọc tiếp
Cho tam giác ABC có B = 70° ; C = 50° nội tiếp trong đường tròn ( O ) .
a ) Tính số đo cung BC .
b ) Gọi AD , BE , CF lần lượt là các đường phân giác của các góc A , B , C . Tính : • Số đo các góc BEC , BED và FDE . • Số đo các cung CBF ; BCE . .
c ) Cho BC = 6 cm . Tính bán kính đường tròn ( O ) .
Cho tam giác ABC có góc A = 60 độ , nội tiếp (O,R)
a , tính số đo cung BC
b , tính độ dài dây BC và độ dài cung BC theo R
c , tính diện tích hình quạt ứng với góc ở tâm BOC theo R
Cho tam giác nhọn ABC nội tiếp đường tròn(O). Các cung nhỏ AB, BC, CA có số đo lần lượt là
x
+
75
0
,
2
x
+
25
0
,
3
x
-
22
°
. Một góc của tam giác ABC có số đo là:
(
A
)
57
°
5...
Đọc tiếp
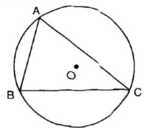
Cho tam giác nhọn ABC nội tiếp đường tròn(O). Các cung nhỏ AB, BC, CA có số đo lần lượt là x + 75 0 , 2 x + 25 0 , 3 x - 22 ° . Một góc của tam giác ABC có số đo là:
( A ) 57 ° 5 ( B ) 59 ° ; ( C ) 61 ° ; ( D ) 60 °
Hãy chọn câu trả lời đúng.
Các cung 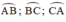 tạo thành một đường tròn
tạo thành một đường tròn
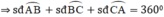
⇒ x + 75 ° + 2 x + 25 ° + 3 x − 22 ° = 360 ° ⇒ 6 x = 282 ° ⇒ x = 47 °
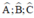 là các góc nội tiếp chắn các cung
là các góc nội tiếp chắn các cung 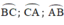
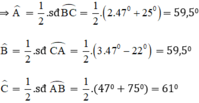
Vậy chọn đáp án C.
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC nội tiếp đường tròn(O). Các cung nhỏ AB, BC, CA có số đo lần lượt là
x
+
75
0
,
2
x
+
25
0
,
3
x
−
22
0
. Một góc của tam giác ABC có số đo là:
(
A
)
57
°
5
;
(
B
)...
Đọc tiếp
Cho tam giác nhọn ABC nội tiếp đường tròn(O). Các cung nhỏ AB, BC, CA có số đo lần lượt là x + 75 0 , 2 x + 25 0 , 3 x − 22 0 . Một góc của tam giác ABC có số đo là:
( A ) 57 ° 5 ; ( B ) 59 ° ; ( C ) 61 ° ; ( D ) 60 °
Hãy chọn câu trả lời đúng.
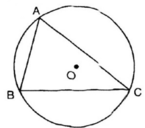
Các cung 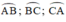 tạo thành một đường tròn
tạo thành một đường tròn
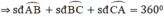
⇒ x + 75 ° + 2 x + 25 ° + 3 x − 22 ° = 360 ° ⇒ 6 x = 282 ° ⇒ x = 47 °
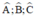 là các góc nội tiếp chắn các cung
là các góc nội tiếp chắn các cung 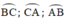
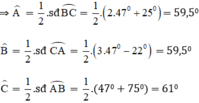
Vậy chọn đáp án C.
Đúng 0
Bình luận (0)
a) Cho tam giác ABC vuông tại A. Tia phân giác BD chia AC thành 2 phần sao cho CD = 2AD. Tính số đo góc ABC.
b) Cho tam giác ABC có A = 70o, B = 60o. Đường tròn tâm O ngoại tiếp tam giác ABC. Tính số đo góc AOB.
a)
Theo tính chất đường phân giác áp dụng cho \(\Delta ABC\) có BD là phân giác góc ABC \(\Rightarrow\frac{AB}{BC}=\frac{AD}{DC}=\frac{1}{2}\)
\(\Delta ABC\) vuông tại A\(\Rightarrow\tan B=\frac{AB}{BC}=\frac{1}{2}\Rightarrow\widehat{B}\approx27\)
b,
Thấy \(\widehat{ACB}\) nội tiếp \(\left(O\right)\) chắn cung AB nhỏ
\(\Rightarrow\widehat{ACB}=\frac{1}{2}sđ\overline{AB}\left(1\right)\)
Thấy \(\widehat{AOB}\) chắn cung AB nhỏ \(\Rightarrow\widehat{AOB}=sđ\overline{AB}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\widehat{AOB}=2\widehat{ACB}=2\left(180^o-70^o-60^o\right)=2.50^o=100^o\)
Đúng 0
Bình luận (0)
Cho ∆ABC cân nội tiếp đường tròn (O), cung nhỏ BC có số
đo bằng 100 độ
. Tia AO cắt cung nhỏ BC ở E.a) Tính số đo các góc ở tâm BOE, COE.b) Tính số đo các cung nhỏ
AB CD , .
Giúp em gấp với
Thực sự là e đg rất gần
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB = 3 cm, BC = 6 cm.
a) Tính độ dài cạnh AC, số đo góc B và góc C
b) Vẽ (O) ngoại tiếp tam giác ABC. Đường cao AH của tam giác ABC cắt (O) tại D. Chứng minh BC là đường trung trực của AD
c) Tiếp tuyến tại D của (O) cắt BC tại E. Chứng minh EA là tiếp tuyến của (O)
d) Chứng minh EA^2 = EB.EC
mình hướng dẫn nhé
a) sử dụng hệ thức lượng trong \(\Delta\) vuông. Đây là tính cạnh
còn tính góc thì sử dụng hệ thức giữa cạnh và góc
áp dụng công thức là làm đc đấy mà
b) sử dụng tính chất 2 tiếp tuyến cắt nhau rồi xét \(\Delta\)có tia phân giác đồng thời là đường cao, đường trung trực
c) chứng minh tiếp tuyến ta chứng minh \(\Delta\)vuông
d) mình chưa nghĩ ra nhưng chắc là sử dụng hệ thức lượng quy về \(\Delta\)
vuông
Đúng 0
Bình luận (0)
Bài 4: cho tam giác cân ABC nội tiếp đường tròn (O), cung nhỏ BC có số đo bằng 1000. Tia AO cắt cung nhỏ AC ở E.
a, Tính số đo các góc ở tâm BOE, COE
b, Tính số đo các cung nhỏ AB, AC.














