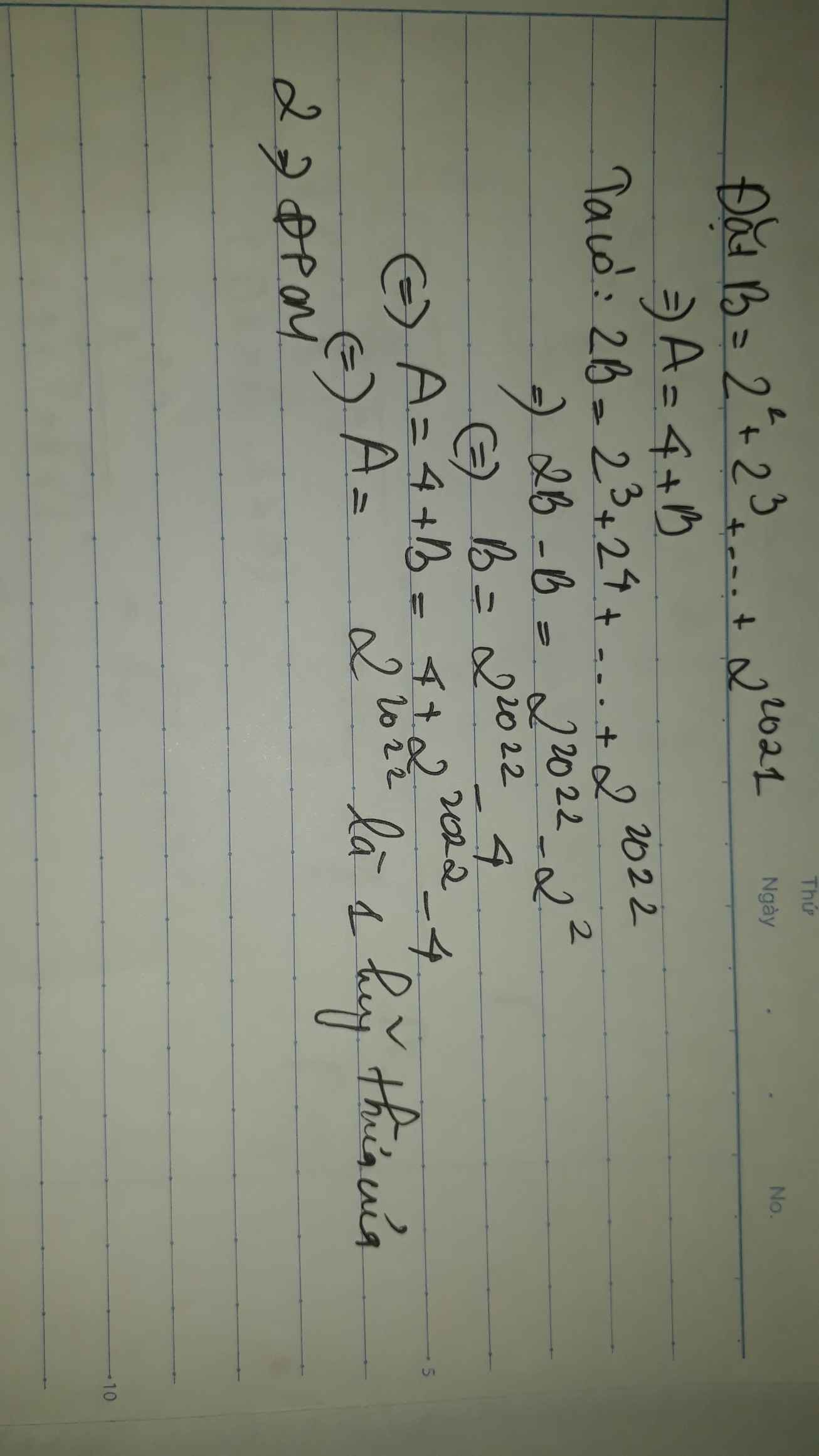chứng minh rằng A là một lũy thừa của 2 với A=4+2^3+2^4+....+2^2004

Những câu hỏi liên quan
a) Cho A=1-3+3^2-3^3+...-3^2003+3^2004.Chứng minh 4A-1 là lũy thừa của 3
b) Chứng minh rằng A là một lũy thừa của 2 với A=4+2^3+2^4+...+2^2003+2^2004
Từng bài 1 thôi nhs!
a) 3A = 3 - 32 + 33 - 34 + ... -32004+ 32005
3A + A = 3 - 32 + 33 -34 + ... -32004 + 32005 +1 - 3 + 32- 33 + 34 - ....-32003+32004
4A = 32005 + 1
=> 4A - 1 = 32005 là lũy thừa của 3
=> ĐPCM
Đúng 0
Bình luận (0)
đề có thiếu ko đó
A = 4 + 23 + 24 + 25 + ...+ 22003 + 22004
đặt B = 23 + 24 + 25 + ...+ 22003 + 22004
2B= 24 + 25 + 26 + ....+ 22004 + 22005
2B-B= ( 24 + 25 + 26 + ....+ 22004 + 22005 ) - ( 23 + 24 + 25 + ...+ 22003 + 22004 )
B = 24 + 25 + 26 + ....+ 22004 + 22005 - 23 - 24 - 25 - ...- 22003 - 22004
B = 22005 - 23
B = 22005 - 8
=> A = 4 + B = 4 + 22005 - 8 = 22005 - 4 = .....
Đúng 0
Bình luận (0)
Chứng minh rằng A là 1 lũy thừa của 2 với:
A= 4+22+23+24+...+22003+22004
\(A=4+2^2+2^3+2^4+...+2^{2004}\)
\(2A=8+2^3+2^4+2^5+...+2^{2004}+2^{2005}\)
\(A=2A-A=2^{2005}\)
Vậy \(A=4+2^2+2^3+2^4+2^5+...+2^{2004}\)là 1 lũy thừa của 2
Đúng 0
Bình luận (0)
a] Chứng minh rằng a là 1 lũy thừa của 2 với A= 4+2^2+2^3+2^4+...+2^20
b] Chứng minh rằng 2A+3 là 1 lũy thừa của 3 với A=3+3^2+3^3+...3+3^100
a, Có 2A = 4.2+2^3+2^4+...+2^21
A=2A-A=(4.2+2^3+2^4+...+2^21)-(4+2^2+2^3+...+2^20) = 4.2 + 2^21 - 4 - 2^2 = 2^21
=> A là lũy thừa cơ số 2
b, Có 3A=3^2+3^3+3^4+...+3^101
2A=3A-A=(3^2+3^3+3^4+....+3^101)-(3+3^2+3^3+....+3^100) = 3^101-3
=> 2A+3 = 3^101-3+3 = 3^101
=> A là lũy thừa của 3
k mk nha
Đúng 0
Bình luận (0)
a chứng minh rằng A là một lũy thừa của 2 với
\(A=4+2^2+2^3+2^4+...+2^{20}\)
b chứng minh rằng 2A + 3 là một lũy thừa của 3 với
\(A=3+3^2+3^3+...+3^{100}\)
A=4+22+23+...+220
Đặt B=22+23+...+220
=>2B=23+24+...+221
=>2B-B=221-22=221-4
=>A=4+B=4+221-4=221
=>A là lũy thừa của 2(ĐPCM)
b)A=3+32+33+...+3100
=>3A=32+33+...+3101
=>3A-A=3101-3
=>2A=3101-3
=>2A+3=3101-3+3=3101
Vậy 2A+3 là lũy thừa của 3(ĐPCM)
Đúng 0
Bình luận (0)
a/
\(2A=8+2^3+...+2^{21}\)
\(2A-A=A=2^{21}+8-4-2^2=2^{21}\)
b/
\(3B=3^2+3^3+...+3^{101}\)
\(\Rightarrow3B-B=2B=3^{101}-3\)
\(\Rightarrow2B+3=3^{101}\)
Đúng 0
Bình luận (0)
vì sao các bạn ghi đc số mũ zậy, chỉ mình vs
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
chứng minh rằng A là một lũy thừa của 2 với : A = 4+2^2+2^3+...+2^2021
Đặt \(B=2^2+2^3+...+2^{2021}\)
\(\Leftrightarrow2\cdot B=2^3+2^4+...+2^{2022}\)
\(\Leftrightarrow B=2^{2022}-4\)
\(\Leftrightarrow A=B+4=2^{2022}\)
Đúng 0
Bình luận (0)
chứng minh rằng A là một lũy thừa của 2 với : A = 4+2^2+2^3+2^4+...+2^20
A=2^2+2^2+2^3+2^4+....+2^20=2*2^2+2^3+2^4+...+2^20=2^3+2^3+2^4+...+2^20=2^21
Đúng 0
Bình luận (0)
A = 4 + 22 + 23 + 24 + .... + 220.
Giải : A = 4 + 22 + 23 + 24 + ..... + 220
2A = 8 + 23 + 24 + .... + 220 + 221
Suy ra : 2A - A = 221 + 8 - ( 4 + 22 )
Vậy A = 221
Đúng 1
Bình luận (0)
A = 4 + 2^2 + 2^3 + 2^4 +.....+ 2^20
2A = 8 + 2^3 + 2^4 +....+2^21
2A - A = 8 + 2^3 + 2^4 + 2^5 +....+2^21 - 4 - 2^2 - 2^3 - 2^4 - ...- 2^20
loại trừ dần ta còn
A = 8+2^21 - 4- 2^2 = 8 + 2^21 - 8 = 2^21
Kết luận : A là lũy thừa của 2
Đúng 0
Bình luận (0)
Chứng minh rằng A là một lũy thừa của 2 với A= 4 + 2^3 + 2^4 + 2^5 +..........+2^2003 + 2^2004
Cho S = 5 + 5^2 + 5^3 +.......+ 5^96
Tìm chữ số tận cùng của S
Ai giải dc sẽ có like mà giải cho đúng nha
Chia tổng trên thành 16 nhóm, mỗi nhóm 6 số hạng ta có:
S=(5+52+53+54+55+56)+56(5+52+53+54+55+56)+...+590(5+52+53+54+55+56)
=(5+52+53+54+55+56)(1+56+...+590)
Ta có
5+52+53+54+55+56=5(1+53)+52(1+53)+53(1+53)=126(5+52+53)⋮126
→S⋮126
S⋮5.2=10
Vậy tận cùng là 0
Đúng 0
Bình luận (0)
Chứng minh rằng A là một lũy thừa của 2,với;
A=4+2^2+2^3+2^4+ ......... +2^50
chứng minh rằng A là một lũy thừa của 2 với;A=4+2 mũ 2+2 mũ 3+......+2 mũ 20
\(A=2^2+2^2+2^3+...+2^{20}\\ 2A=2^3+2^3+2^4+...+2^{21}\\ 2A-A=\left(2^3+2^3+2^4+...+2^{21}\right)-\left(2^2+2^2+2^3...+2^{20}\right)\\ A=2^{21}+2^3-2^2-2^2\\ A=2^{21}+8-4-4=2^{21}\left(đpcm\right)\)
Đúng 3
Bình luận (0)