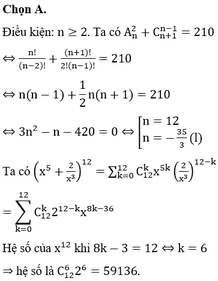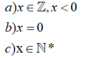x5=210

Những câu hỏi liên quan
Với n là số nguyên dương thỏa mãn
A
n
2
+
C
n
+
1
n
-
1
210
, hệ số của số hạng chứa
x
12
tr...
Đọc tiếp
Với n là số nguyên dương thỏa mãn A n 2 + C n + 1 n - 1 = 210 , hệ số của số hạng chứa x 12 trong khai triển x 5 + 2 x 3 n bằng
A. 59136.
B. 59130 x 12 .
C. 59130.
D. 59136 x 12 .
Thực hiện phép tính:
a. 142-[50-(\(2^3\)x10-\(2^3\)x5)]
b. 375:{32[4+(5x\(3^2\)-42)]} - 14
c.{210:[16+3.(6+3x\(2^2\))]} - 3
d. 500-{5x[409-(\(2^3\) x3-21)\(^2\)] - 1724
a: Ta có: \(142-\left[50-\left(2^3\cdot10-2^3\cdot5\right)\right]\)
\(=142-\left[50-80+40\right]\)
=142-10
=132
Đúng 1
Bình luận (0)
a. 142 - [50-(23.10-23.5)]
= 142 - [ 50 - ( 8 . 10 - 8 . 5 )]
= 142 - [ 50 - ( 80 - 40 )]
= 142 - [ 50 - 40 ]
= 142 - 10 = 132
b. 375 : { 32[ 4+(5.32 - 42 )]} - 14
= 375 : { 32[4+(5.9 - 42 )]} - 14
= 375 : { 32[4 + ( 45 - 42 )]} - 14
= 375 : {32[4+3]} - 14
= 375 : 224 - 14
c.{210 : [ 16+3.(6+3.2^2)]} - 3
= {210 : [ 16 + 3.(6+3.4)]} - 3
= { 210 :[16+3.(6+12)]}-3
= {210 : [ 16+3.18)]} - 3
= { 210 : [ 16 + 54]} - 3
= { 210 : 70 } - 3
= 30 - 3 = 27
d.500-{5.[409-(2^3 . 3-21^2)] - 1724}
= 500-{5.[409-(8 . 63 - 21^2] - 1724}
= 500 - { 5.[409- (504 - 441) - 1724}
= 500 -{ 5.[ 409 - 63 ] - 1724}
= 500 - { 5.346 - 1724}
= 500 - { 1720 - 1724 }
= 500 - 6
= 494
Đúng 2
Bình luận (1)
11111111111111111111111111111111111111111111111111111111111 x 2222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222 x 5 x5 x5 x5 x5 x5 x5 x5 x55x5x55x5x5x5x5x5x5x5x5xx5x5x5x5x55x5x5x5x5x55x5555xxxx55x0x66666666x6x6x6x6x6x66x6x6x6x = ........
mik chỉ k cho 2 người thôi nhé
Cho phân số
x
5
. Với giá trị nguyên nào của x thì ta có:
a
)
x
5
0
b
)
x
5
0...
Đọc tiếp
Cho phân số x 5 . Với giá trị nguyên nào của x thì ta có:
a ) x 5 < 0 b ) x 5 = 0 c ) x 5 > 0 d ) x 5 = 1 e ) 0 < x 5 < 1 f ) 1 < x 5 ≤ 2
a ) x ∈ ℤ , x < 0 b ) x = 0 c ) x ∈ ℕ *
d) x = 5
e) x ∈ {1;2;3;4}
f) x ∈ {6;7;8;9;10}
Đúng 0
Bình luận (0)
Tính tổng
A=1 x 5 x 51 x52 x 53x54x55x56x57x58x59x510
kết quả là 5 ^ 56
bạn ơi bằng
5mũ 56
học tốt nha
Cho phân số
x
5
. Với giá trị nguyên nào của x thì ta có:a)
x
5
0
b)
x
5
0
c)
x
5
0
Đọc tiếp
Cho phân số x 5 . Với giá trị nguyên nào của x thì ta có:
a) x 5 < 0
b) x 5 = 0
c) x 5 > 0
Cho phân số
x
5
. Với giá trị nguyên nào của x thì ta có:a)
x
5
1
b)
0
x
5
1
c)
1
x
5
≤
2
Đọc tiếp
Cho phân số x 5 . Với giá trị nguyên nào của x thì ta có:
a) x 5 = 1
b) 0 < x 5 < 1
c) 1 < x 5 ≤ 2
xét các số nguyên x1;x2;...;x5 thỏa mãn (1 + x1)(1 + x2)···(1 + x5) = (1−x1)(1−x2)···(1−x5) = x. chứng minh rằng xx1x2...x5=0
Đề bài:
Trong trường hợp này, trong tích \(P = \left(\right. 1 + x_{1} \left.\right) \left(\right. 1 + x_{2} \left.\right) \hdots\), sẽ có một thừa số bằng 0.
⇒ \(x = 0\).
Do đó \(x x_{1} x_{2} \hdots x_{5} = 0\).Nếu có một \(x_{i} = - 1\), tương tự, \(x = 0\).
⇒ Kết quả đúng.Nếu không có số nào bằng \(\pm 1\):
Khi đó (1) hoàn toàn xác định.
Lưu ý rằng \(\frac{1 + x_{i}}{1 - x_{i}}\) là một phân số không bằng 0.
Tích của 5 phân số bằng 1.
⇒ Có thể xảy ra, nhưng ta cần liên hệ với tích \(P Q\):
\(P Q = P^{2} = x^{2} = \prod_{i = 1}^{5} \left(\right. 1 - x_{i}^{2} \left.\right) .\)
Nếu không có số nào bằng \(\pm 1\), thì mỗi \(1 - x_{i}^{2} \neq 0\). Vế phải khác 0, suy ra \(x \neq 0\).
Nhưng khi đó \(x^{2} = \prod \left(\right. 1 - x_{i}^{2} \left.\right)\).
Nghĩa là \(x\) chia hết cho tích \(\prod x_{i}\) (do đồng dư mod \(x_{i}\), lập luận chia hết)…
Kết quả là hoặc \(x = 0\) hoặc một trong các \(x_{i} = 0\).
⇒ Trong cả hai trường hợp, \(x x_{1} x_{2} \hdots x_{5} = 0\).Kết luận:
Xét các số nguyên \(x_{1} , x_{2} , \ldots , x_{5}\) thỏa mãn
\(\left(\right. 1 + x_{1} \left.\right) \left(\right. 1 + x_{2} \left.\right) \hdots \left(\right. 1 + x_{5} \left.\right) \textrm{ }\textrm{ } = \textrm{ }\textrm{ } \left(\right. 1 - x_{1} \left.\right) \left(\right. 1 - x_{2} \left.\right) \hdots \left(\right. 1 - x_{5} \left.\right) \textrm{ }\textrm{ } = \textrm{ }\textrm{ } x .\)
Chứng minh rằng
\(x \cdot x_{1} x_{2} \hdots x_{5} = 0.\)
Lời giải:Gọi
\(P = \prod_{i = 1}^{5} \left(\right. 1 + x_{i} \left.\right) , Q = \prod_{i = 1}^{5} \left(\right. 1 - x_{i} \left.\right) .\)
Theo đề: \(P = Q = x\).
Bước 1: Xét tích \(P Q\)\(P Q = \prod_{i = 1}^{5} \left(\right. 1 + x_{i} \left.\right) \left(\right. 1 - x_{i} \left.\right) = \prod_{i = 1}^{5} \left(\right. 1 - x_{i}^{2} \left.\right) .\)
Bước 2: Sử dụng giả thiết \(P = Q\)Từ \(P = Q\), suy ra:
\(\prod_{i = 1}^{5} \left(\right. 1 + x_{i} \left.\right) = \prod_{i = 1}^{5} \left(\right. 1 - x_{i} \left.\right) .\)
Chuyển vế:
\(& \prod_{i = 1}^{5} \frac{1 + x_{i}}{1 - x_{i}} = 1. & & (\text{1})\)
Bước 3: Phân tích trường hợpNếu có một \(x_{i} = 1\), thì vế phải (1) có mẫu số bằng 0 → đẳng thức chỉ đúng khi đồng thời tử số cũng bằng 0, tức là có một \(x_{j} = - 1\).Trong trường hợp này, trong tích \(P = \left(\right. 1 + x_{1} \left.\right) \left(\right. 1 + x_{2} \left.\right) \hdots\), sẽ có một thừa số bằng 0.
⇒ \(x = 0\).
Do đó \(x x_{1} x_{2} \hdots x_{5} = 0\).Nếu có một \(x_{i} = - 1\), tương tự, \(x = 0\).
⇒ Kết quả đúng.Nếu không có số nào bằng \(\pm 1\):
Khi đó (1) hoàn toàn xác định.
Lưu ý rằng \(\frac{1 + x_{i}}{1 - x_{i}}\) là một phân số không bằng 0.
Tích của 5 phân số bằng 1.
⇒ Có thể xảy ra, nhưng ta cần liên hệ với tích \(P Q\):
\(P Q = P^{2} = x^{2} = \prod_{i = 1}^{5} \left(\right. 1 - x_{i}^{2} \left.\right) .\)
Nếu không có số nào bằng \(\pm 1\), thì mỗi \(1 - x_{i}^{2} \neq 0\). Vế phải khác 0, suy ra \(x \neq 0\).
Nhưng khi đó \(x^{2} = \prod \left(\right. 1 - x_{i}^{2} \left.\right)\).
Nghĩa là \(x\) chia hết cho tích \(\prod x_{i}\) (do đồng dư mod \(x_{i}\), lập luận chia hết)…
Kết quả là hoặc \(x = 0\) hoặc một trong các \(x_{i} = 0\).
⇒ Trong cả hai trường hợp, \(x x_{1} x_{2} \hdots x_{5} = 0\).Kết luận:
Dù xảy ra trường hợp nào thì ta luôn có:
\(x \cdot x_{1} x_{2} \hdots x_{5} = 0.\)
Đúng 0
Bình luận (0)
TỊM x1+x2+x3+x4+x5+xx6
x1+x2=x3+x4=x5+x6=2bieestx1+x2+x3+x4+X5+x6=0
cho x1, x2, x3, x4, x5 thuộc tập hợp số nguyên
biết x1 + x2 + x3 + x4 + x5=0 và x1+ x2 = x3+ x4 = x4+ x5=2
tính x3, x4, x5