cho tam giác ABC với AD là đường phân giác của góc A Biết AB -= 4cm,AC=6cm,BC=5cm . Tính BD , CD

Những câu hỏi liên quan
Bài 2 (4,5 điểm) Cho tam giác ABC nhọn, AD là đường phân giác. Trên tia đối của tia DA
lấy điểm E sao cho góc AEB = góc ACB.
a) Biết AB = 4cm, AC = 6cm, BC = 8cm. Tính BD, CD.
b) Chứng minh: tam giác DEB đồng dạng với tam giác ADC và tam giác ABE đồng
dạng với tam giác ADC.
c) Chứng minh: AC. AB = AD. AE và AD' = AB.AC- DB.DC.
d) Chứng minh ABE+ACE = 180°.
a: Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
=>BD/2=CD/3=(BD+CD)/(2+3)=8/5=1,6
=>BD=3,2cm; CD=4,8cm
b: Xét ΔDEB và ΔDCA có
góc DEB=góc DCA
góc EDB=góc CDA
=>ΔDEB đồng dạng với ΔDCA
Xét ΔABE và ΔADC có
góc AEB=góc ACD
góc BAE=góc DAC
=>ΔABE đồng dạng với ΔADC
c: ΔABE đồng dạng với ΔADC
=>AB/AD=AE/AC
=>AB*AC=AD*AE
d: góc ACB=góc AEB
=>ABEC nội tiếp
=>góc ABE+góc ACE=180 độ
Đúng 0
Bình luận (0)
cho tam giác ABC có số đo AB=4cm, BC=6cm, AC=5cm. Biết AD là phân giác của góc BAC Tính độ dài BD
hỗ trợ baì này giúp mk với
cho tam giác ABC có AB =4cm,AC=5cm,BC=6cm. AD là đường phân giác tam giác ABC
a) Tính BD,CD
b) kẻ DE//AC , DK//AB . Tính các cạnh tứ giác AEDK
cho tam giác ABC có AB =4cm,AC=5cm,BC=6cm. AD là đường phân giác tam giác ABC
a) Tính BD,CD
b) kẻ DE//AC , DK//AB . Tính các cạnh tứ giác AEDK
cho tam giác ABC có AB =4cm,AC=5cm,BC=6cm. AD là đường phân giác tam giác ABC
a) Tính BD,CD
b) kẻ DE//AC , DK//AB . Tính các cạnh tứ giác AEDK
cho tam giác ABC có AB =4cm,AC=5cm,BC=6cm. AD là đường phân giác tam giác ABC
a) Tính BD,CD
b) kẻ DE//AC , DK//AB . Tính các cạnh tứ giác AEDK
cho tam giác ABC có AB =4cm,AC=5cm,BC=6cm. AD là đường phân giác tam giác ABC
a) Tính BD,CD
b) kẻ DE//AC , DK//AB . Tính các cạnh tứ giác AEDK
a: Xét ΔABC có AD là phân giác
nên DB/AB=DC/AC
=>DB/4=DC/5=(DB+DC)/(4+5)=6/9=2/3
=>DB=8/3cm; DC=10/3cm
b: Xét ΔBAC có DK//AB
nên DK/AB=CD/CB
=>DK/4=10/3:6=10/18=5/9
=>DK=20/9cm
Xét ΔBAC có DE//AC
nên DE/AC=BD/BC
=>DE/5=8/3:6=8/18=4/9
=>DE=20/9cm
Xét tứ giác AEDK có
AE//DK
AK//DE
=>AEDK là hbh
mà AD là phân giác
nên AEDK là hình thoi
=>AE+DE=DK=AK=20/9cm
Đúng 0
Bình luận (0)
Cho tam giác ABC có AD là tia phân giác của góc BAC. Biết AB = 3cm, BD = 4cm, CD = 6cm. Tính AC?
A. 4cm
B. 5cm
C. 6cm
D. 4,5cm
Theo tính chất tia phân giác của góc ta có:
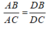
Suy ra:

Chọn đáp án D
Đúng 0
Bình luận (0)
cho tam ABC vuông tại A ,BD là đường phân giác của góc B.Tính AB ,BC biết AD=4cm,CD=5cm
vì BD là tia phân giác nên ta có:
AD/DC = AB/BC = 4/5
mà BC^2 = AB^2 + AC^2 ( tam giác ABC vuông tại A )
Nên : AB/căn bậc hai(AB^2+ 9^2) = 4/5
=> 5AB = 4*canbạc hai(AB^2 + 81)
<=>25AB^2 = 16*(AB^2+81)
<=> 9AB^2 =1296
<=> AB^2 = 144
=> AB = 12 cm
Đúng 0
Bình luận (0)














