Chứng minh góc ACD=ACB, biết AB=AD, góc ABC=ADC=90°

Những câu hỏi liên quan
Cho Hình 43 có AB = AD, \(\widehat {ABC} = \widehat {ADC} = 90^\circ \). Chứng minh \(\widehat {ACB} = \widehat {ACD}\).
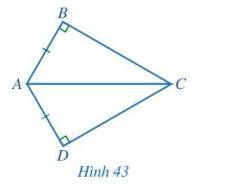
Xét hai tam giác vuông ABC và ADC có: AB = AD, AC chung.
Nên \(\Delta ABC = \Delta ADC\) (cạnh huyền - cạnh góc vuông) nên \(\widehat {ACB} = \widehat {ACD}\) (2 góc tương ứng)
Đúng 1
Bình luận (0)
bài 49 : Cho tam giác ABC có góc ABC = góc ACB và có đường phân giác AD
a) Góc ADB và góc ADC là góc ngoài của những tam giác nào ? Chứng minh góc ADB = góc ADC
2) Chứng minh AB = AC
help me !!!!!!!!!!!!!!!!!!!!!!!!!!!
bài 49 : Cho tam giác ABC có góc ABC = góc ACB và có đường phân giác AD
a) Góc ADB và góc ADC là góc ngoài của những tam giác nào ? Chứng minh góc ADB = góc ADC
2) Chứng minh AB = AC
help me !!!!!!!!!!!!!!!!!!!!!!!!!!!
1. Cho tam giác ABC có góc ABC 70 độ, góc ACB 40 độ.Vẽ tia Cx là tia đối của tia CB. Vẽ tia Cy là tia phân giác của góc Acx.1) Tính góc Acx, góc xAy.2) Chứng minh rằng: AB//Cy.2. Cho hình vẽ, biết góc BAC + góc ACD 180 độ ; góc BDC 70 độ.1) Chứng minh rằng: AB//CD.2) Tính góc ABD.3. Cho hình vẽ, biết góc BAD + góc ADC 180 độ ; góc ABC 90 độ.1) Chứng minh rằng: AB//CD2) Chứng minh rằng: BC vuông góc với CD.Giúp mình nhanh nhé!!!
Đọc tiếp
1. Cho tam giác ABC có góc ABC =70 độ, góc ACB =40 độ.Vẽ tia Cx là tia đối của tia CB. Vẽ tia Cy là tia phân giác của góc Acx.
1) Tính góc Acx, góc xAy.
2) Chứng minh rằng: AB//Cy.
2. Cho hình vẽ, biết góc BAC + góc ACD = 180 độ ; góc BDC = 70 độ.
1) Chứng minh rằng: AB//CD.
2) Tính góc ABD.
3. Cho hình vẽ, biết
góc BAD + góc ADC = 180 độ ; góc ABC = 90 độ.
1) Chứng minh rằng: AB//CD
2) Chứng minh rằng: BC vuông góc với CD.
Giúp mình nhanh nhé!!!
cho đường tròn tâm o đường kính ab dây cd//ab. cd cùng chiều tia ab. chứng minh: a) góc adc = góc bcd b) góc acd = góc adc =90
Cho AC =8cm , AD= 9,6cm , Góc ABC=90độ. Góc ACB=54 độ va góc ACD =74 độ. Hãy tính a) AB
b) góc ADC
Cho góc xAy có tia phân giác là Ad. Trên Ax, Ay lấy lần lượt hai điểm B và D sao cho AB AD. C là một điểm trên Ad sao cho góc ABC tù.a) CMR: tam giác ACB tam giác ACDb) So sánh: ACB và ACD; BC và DCc) Vẽ đường tròn tâm C, bán kính CB, cắt Ax tại điểm E. Hãy chứng tỏ hai tam giác AEC, ADC có hai cặp cạnh và một cặp góc bằng nhau. Với kết quả đó có kết luận ngay hai tam giác AEC, ADC có bằng nhau không? Vì sao?
Đọc tiếp
Cho góc xAy có tia phân giác là Ad. Trên Ax, Ay lấy lần lượt hai điểm B và D sao cho AB= AD. C là một điểm trên Ad sao cho góc ABC tù.
a) CMR: tam giác ACB = tam giác ACD
b) So sánh: ACB và ACD; BC và DC
c) Vẽ đường tròn tâm C, bán kính CB, cắt Ax tại điểm E. Hãy chứng tỏ hai tam giác AEC, ADC có hai cặp cạnh và một cặp góc bằng nhau. Với kết quả đó có kết luận ngay hai tam giác AEC, ADC có bằng nhau không? Vì sao?
Cho hình thang ABCD có góc A =góc D = 90°,CD = 2AD = 2AB, cho AC = 25.
a) Tính góc ACD.
b) Tính AB, AD,CD.
c) Vẽ DH vuông góc AC. Tính DH và chứng minh góc ABH = góc ACB.
a) Xét tam giác \(ADC\)vuông tại \(D\):
\(tan\widehat{ACD}=\frac{AD}{DC}=\frac{1}{2}\Rightarrow\widehat{ACD}=arctan\frac{1}{2}\)
b) Xét tam giác \(ADC\)vuông tại \(D\):
\(AC^2=AD^2+DC^2=AD^2+4AD^2=5AD^2\)
\(\Leftrightarrow AD=\sqrt{\frac{AC^2}{5}}=\sqrt{\frac{25^2}{5}}=5\sqrt{5}\left(cm\right)\)
\(AB=AD=5\sqrt{5}\left(cm\right),CD=2AD=10\sqrt{5}\left(cm\right)\).
c) Xét tam giác \(ADC\)vuông tại \(D\):
\(DH=\frac{AD.DC}{AC}=\frac{10\sqrt{5}.5\sqrt{5}}{25}=10\left(cm\right)\)
\(AH=\frac{AD^2}{AC}=\frac{AB^2}{AC}\Leftrightarrow\frac{AB}{AC}=\frac{AH}{AB}\)
Xét tam giác \(ABH\)và tam giác \(ACB\):
\(\widehat{A}\)chung
\(\frac{AB}{AC}=\frac{AH}{AB}\)
suy ra \(\Delta ABH~\Delta ACB\left(c.g.c\right)\)
\(\Rightarrow\widehat{ABH}=\widehat{ACB}\)
cho đường tròn tâm o đường kính ab dây cd//ab. cd cùng chiều tia ab. chứng minh: a) góc adc = góc bcd b) góc acd = góc adc =90cho đường tròn tâm o đường kính ab dây cd//ab. cd cùng chiều tia ab. chứng minh: a) góc adc = góc bcd b) góc acd = góc adc =90










