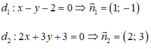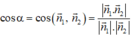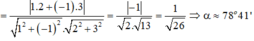Cho 2 đường thẳng d1= 2x-y-2=0, d2= x+y+3=0 và M(3;0). Viết phương trình đường thẳng d đi qua M, cắt d1,d2 lând lượt tại 2 điểm A và B sao cho M là trung điểm

Những câu hỏi liên quan
Cho đường thẳng d1: 2x+y-2=0 và đường thẳng d2: x-y+2=0 và d3: x+2y+3=0. Tìm điểm M thuộc d1 cách đều d2 và d3
Cho 2 đường thẳng: (d1) mx - y = 1 ; (d2) 2x + y = 3
a. tìm m để (d1) cắt (d2)
b. tìm m để (d1) cắt (d2) tại A(x;y) sao cho x > 0; y > 0
Cho hai đường thẳng d1: 2x + 2 3 y + 5 = 0 và d2: y - 6 = 0. Góc giữa d1 và d2 có số đo bằng:
A. 30 °
B. 45 °
C. 60 °
D. 135 °
Đáp án: A
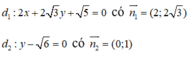
Gọi α là góc giữa hai đường thẳng d1, d2
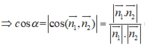
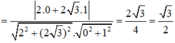
⇒ α = 30 °
Đúng 0
Bình luận (0)
Cho hàm số \(y=\dfrac{2x-3}{x-2}\)có đồ thị (C) và hai đường thẳng d1: \(y-2=0\)và d2: \(x-2=0\).Tiếp tuyến của đồ thị (C) cắt các đường thẳng d1, d2 lần lượt tại A,B sao cho độ lại AB ngắn nhất. Khi đó AB2 bằng
Cho 3 đường thẳng d1 : 2x+ y -1= 0 ; d2 : x+ 2y+1= 0 và d3 : mx-y-7= 0 Để ba đường thẳng này đồng qui thì m bằng ?
A. m= -6
B. m= 6
C.m= 3
D. m= 2
Đáp án B
+Giao điểm của d1 và d2 là nghiệm của hệ:
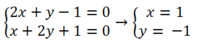
Vậy 2 đường thẳng d1 và d2 tại A( 1 ; -1) .
+Để 3 đường thẳng đã cho đồng quy thì d3 phải đi qua điểm A nên tọa độ A thỏa phương trình d3
Suy ra : m+ 1-7= 0 hay m= 6.
Đúng 0
Bình luận (0)
Bài 1: cho 2 đường thẳng y=(m-3)x+3 (d1) và y= -x+m (d2). Tìm m để (d1)// (d2)
Bài 2: cho 2 đường thẳng y=2x (d1) và y= -x+3 (d2)
a) tìm tọa độ giao điểm A của (d1) và (d2)
b) viết phương trình đường thẳng (d3) qua A và // với đường thẳng y= x+4 (d)
Giải chi tiết dùm mình với ạ :<
BÀI 1
để d1 và d2 // thì: m-3=-1(1) ; m khác 3 (2)
ta có: (1) <=> m=2 (3)
từ (2) và (3) => để d1//d2 thì m = 2
Đúng 0
Bình luận (0)
cho 2 đường thẳng d1: 3x-y-3=0 và d2: x+y+2=0 và M(0,2). viết phương trình đường thẳng d đi qua M cắt d1 và d2 lần lượt tại A và B sao cho B là trung điểm của AM
Giúp mk vs ạ:((
Do A thuộc d1 nên tọa độ có dạng \(A\left(a;3a-3\right)\)
Do B thuộc d2 nên tọa độ có dạng: \(B\left(b;-b-2\right)\)
Áp dụng công thức trung điểm:
\(\Rightarrow\left\{{}\begin{matrix}a+0=2b\\3a-3+2=2\left(-b-2\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a-2b=0\\3a+2b=-3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-\dfrac{3}{4}\\b=-\dfrac{3}{8}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}A\left(-\dfrac{3}{4};-\dfrac{21}{4}\right)\\B\left(-\dfrac{3}{8},-\dfrac{13}{8}\right)\end{matrix}\right.\) \(\Rightarrow\overrightarrow{AB}=\left(\dfrac{3}{8};\dfrac{29}{8}\right)\)
Phương trình d có dạng:
\(29x-3\left(y-2\right)=0\Leftrightarrow29x-3y+6=0\)
Đúng 0
Bình luận (0)
trong mặt phẳng tọa độ oxy cho hai đường thẳng (d1)2x-y+5=0 và (d2) x+y-3=0 cắt nhau tại i. phương trình đường thẳng đi qua m (-2;0) cắt d1, d2 tại a, b sao cho tam giác iab cân tại a có phương trình dạng ax+by+2=0. tính t=a-5b
Góc tạo bởi hai đường thẳng d1: x - y - 2 = 0 và d2: 2x + 3y + 3 = 0 là:
A. 11 ° 19'
B. 78 ° 41'
C. 79 ° 41'
D. 10 ° 19'