Đáp án B
+Giao điểm của d1 và d2 là nghiệm của hệ:
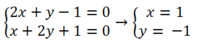
Vậy 2 đường thẳng d1 và d2 tại A( 1 ; -1) .
+Để 3 đường thẳng đã cho đồng quy thì d3 phải đi qua điểm A nên tọa độ A thỏa phương trình d3
Suy ra : m+ 1-7= 0 hay m= 6.
Đáp án B
+Giao điểm của d1 và d2 là nghiệm của hệ:
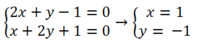
Vậy 2 đường thẳng d1 và d2 tại A( 1 ; -1) .
+Để 3 đường thẳng đã cho đồng quy thì d3 phải đi qua điểm A nên tọa độ A thỏa phương trình d3
Suy ra : m+ 1-7= 0 hay m= 6.
Cho 3 đường thẳng d1: 2x + y – 1 = 0, d2: x + 2y + 1 = 0, d3: mx – y – 7 = 0. Điều kiện của m để ba đường thẳng đồng quy là :
A. m = -6
B. m = 6
C. m = –5
D. m = 5
Cho ba đường thẳng d1: 2x-y-1=0, d2: mx-(m-2)y+m+4=0, d3: x+y-2=0. Giá trị của m để ba đường thẳng đồng quy là
A. m = 0
B. m = 2
C. m = -2
D. m = -6
Cho ba đường thẳng d 1 : x − 2 y + 1 = 0 , d 2 : m x − 3 m − 2 y + 2 m − 2 = 0 , d 3 : x + y − 5 = 0 . Giá trị m để hai đường thẳng d1;d2 cắt nhau tại một điểm nằm trên d3 là
A.m = 0
B.m = 1
C.m = 2
D. không tồn tại m thỏa mãn
Cho ba đường thẳng d 1 : 3 x − 4 y + 1 = 0 , d 2 : 5 x + 3 y − 1 = 0 , d 3 : x + y + 6 = 0 . Số điểm M cách đều ba đường thẳng trên là
A.1
B. 2
C.3
D. 4
Cho hai đường thẳng d 1 : 2 x + 3 y + 1 = 0 , d 2 : m x + 2 m − 2 y − m + 6 = 0 . Giá trị của m để hai đường thẳng song song là
A.m =0
B.m = - 4
C.m = 4
D.không tồn tại m thỏa mãn
Tìm m để ba đường thẳng y = 2x – 3 (d1); y = x – 1 (d2); y = (m − 1)x + 2 (d3) đồng quy.
A. m = 1
B. m = -1
C. m = - 1 2
D. m = 1 2
Cho 2 đường thẳng d1= 2x-y-2=0, d2= x+y+3=0 và M(3;0). Viết phương trình đường thẳng d đi qua M, cắt d1,d2 lând lượt tại 2 điểm A và B sao cho M là trung điểm
Cho 3 đường thẳng (d1) x=1-2t y=1+t, (d2): 3x+4y-4=0, (d3): 4x-3y+2=0 . Tìm điểm M nằm trên (d1) cách đều (d2) và d3
Cho ba đường thẳng
d 1 : 2 x + 3 y = 1 ; d 2 : x - y = 2 ; d 3 : m x + 2 m + 1 y = 2 .
Ba đường thẳng này đồng quy khi:
A. m = 12
B. m = 13
C. m = 14
D. m = 15