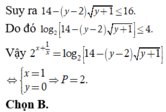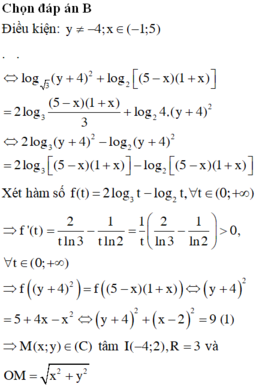cho cặp (x0, y0)thỏa mãn 2(x2 +1)+y2=2y(x+1). Giá trị của biểu thức A =x20+ y02 -5 bằng bao nhiêu
Những câu hỏi liên quan
Cho hệ phương trình
x
+
y
m
-
1
x
2
+
y
2
-
2
x...
Đọc tiếp
Cho hệ phương trình x + y = m - 1 x 2 + y 2 - 2 x - 2 y = - 1 . Tìm m để hệ phương trình có nghiệm x 0 ; y 0 thỏa mãn P = x 0 2 + y 0 2 nhỏ nhất
Hệ phương trình
2
x
+
y
2
−
5
4
x
2
−...
Đọc tiếp
Hệ phương trình 2 x + y 2 − 5 4 x 2 − y 2 + 6 4 x 2 − 4 x y + y 2 = 0 2 x + y + 1 2 x − y = 3 nghiệm x 0 ; y 0 thỏa mãn x 0 > 1 2 . Khi đó P = x 0 + y 0 2 có giá trị là:
A. 1
B. 7 16
C. 3
D. 1 hoặc 7 16
Ta có: 2 x + y 2 − 5 4 x 2 − y 2 + 6 4 x 2 − 4 x y + y 2 = 0 ( 1 ) 2 x + y + 1 2 x − y = 3
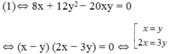
Với x = y ta có 2 ⇒ 3 x + 1 x = 3 ⇔ 3 x 2 - 3 x + 1 = 0 : phương trình vô nghiệm.
Với 2 x = 3 y ta có 2 ⇒ 4 y + 1 2 y = 3 ⇔ 8 y 2 - 6 y + 1 = 0 ⇔ y = 1 2 y = 1 4
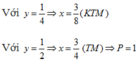
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
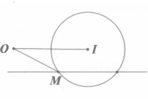
Cho x 0 và số thực y thỏa mãn
2
x
+
1
x
log
2
14
-
y
-
2
y
+
1
. Giá trị của biểu thức
P...
Đọc tiếp
Cho x > 0 và số thực y thỏa mãn 2 x + 1 x = log 2 14 - y - 2 y + 1 . Giá trị của biểu thức P = x 2 + y 2 - x y + 1 bằng
A. 1
B. 2
C. 3
D. 4
Cho ba số thực x, y, z thỏa mãn x+ y – z 2. Biết giá trị nhỏ nhất của biểu thức đạt tại
x
0
;
y
0
;
z
0
. Tính
x
0...
Đọc tiếp
Cho ba số thực x, y, z thỏa mãn x+ y – z = 2. Biết giá trị nhỏ nhất của biểu thức 
đạt tại
x
0
;
y
0
;
z
0
. Tính
x
0
+
y
0
A. 3/2
B. 4
C. 3
D. 5/2
Đáp án D
Phương pháp: Chuyến sang hệ trục tọa độ trong không gian.
Cách giải:
Lấy 
bất kì, M(1;1;1), N(2;1;0)
Ta thấy 
N nằm khác phía so với mặt phẳng
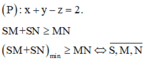
Khi đó, S là giao điểm của MN và (P).
*) Xác định tọa độ của S: 
Phương trình đường thẳng MN: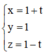 
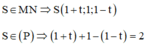
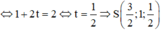
Vậy, biểu thức A đạt GTNN tại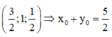 
Đúng 0
Bình luận (0)
Cho số phức
z
x
+
y
i
(
x
,
y
∈
R
)
thỏa mãn
z
-
2
+
i
z
+
2
+
5
i
và biểu thức
H
x...
Đọc tiếp
Cho số phức z = x + y i ( x , y ∈ R ) thỏa mãn z - 2 + i = z + 2 + 5 i và biểu thức H = x 2 + y 2 - 3 y + 1 x 2 + y 2 + 2 x - 2 y + 2 x 2 + y 2 - 2 x - 4 y + 5 đạt giá trị nhỏ nhất. Giá trị của 2x + y bằng
A. -6
B. - 6 + 5
C. - 3 - 5
D. - 6 - 5
Cho hai số thực x, y thỏa mãn:
log
3
(
y
2
+
8
y
+
16
)
+
l
o
g
2
[(
5
−
x
)
(
1
+
x
)
]2log
3
5
+
4
x...
Đọc tiếp
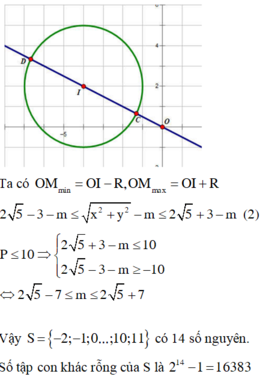
Cho hai số thực x, y thỏa mãn: log 3 ( y 2 + 8 y + 16 ) + l o g 2 [( 5 − x ) ( 1 + x ) ]=2log 3 5 + 4 x − x 2 3 + log 2 ( 2 y + 8 ) 2 . Gọi S là tập các giá trị nguyên của tham số m để giá trị lớn nhất của biểu thức P = x 2 + y 2 − m không vượt quá 10. Hỏi S có bao nhiêu tập con không phải là tập rỗng?
A. 2047
B. 16383
C. 16384
D. 32
Có tất cả bao nhiêu cặp số thực (x,y) sao cho
x
∈
-
1
;
1
và
ln
(
x
-
y
)
x
-
2017
y
+
e
2018
. Biết rằng giá trị lớn nhất của biểu thức...
Đọc tiếp
Có tất cả bao nhiêu cặp số thực (x,y) sao cho x ∈ - 1 ; 1 và ln ( x - y ) x - 2017 y + e 2018 . Biết rằng giá trị lớn nhất của biểu thức P = e 2018 ( y + 1 ) x 2 - 2018 x 2 với ( x ; y ) ∈ S đạt được tại (x0, y0). Mệnh đề nào sau đây đúng?
Đáp án A
Ta có
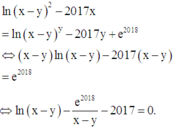
Xét hàm số
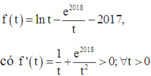
Suy ra f(t) là hàm số đồng biến trên
Khi đó
Lại có
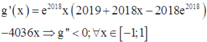
Nên g’(x) là hàm số nghịch biến trên
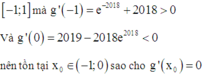
Vậy m a x - 1 ; 1 g ( x ) = g ( x 0 ) hay giá trị lớn nhất của P đạt được khi x 0 ∈ ( - 1 ; 0 )
Đúng 0
Bình luận (0)
Cho
0
≤
x
;
y
≤
1
thỏa mãn
2017
1
-
x
-
y
x
2
+
2018
x
2
-...
Đọc tiếp
Cho 0 ≤ x ; y ≤ 1 thỏa mãn 2017 1 - x - y = x 2 + 2018 x 2 - 2 y + 2019 . Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức S = (4x2 + 3y)(4y2 + 3x) + 25xy. Khi đó M + m bằng bao nhiêu?
Đáp án B
Từ giả thiết
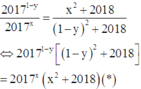
Xét hàm số
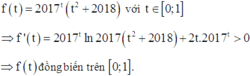
Do đó (*)
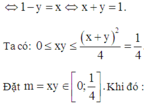
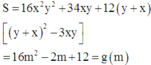
Xét hàm g(m) trên đoạn
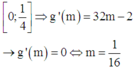
Lúc này
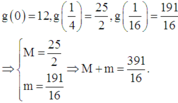
Đúng 0
Bình luận (0)
Xét các số thực x, y thỏa mãn
x
2
+
y
2
≥
4
và
l
o
g
x
2
+
y
2
(
4
x
-
2
y
)
≥
1
. Giá trị lớn nhất của biểu thức P3x+4y-5 là với a, b là các số nguyên. Tính
T
a
3...
Đọc tiếp
Xét các số thực x, y thỏa mãn x 2 + y 2 ≥ 4 và l o g x 2 + y 2 ( 4 x - 2 y ) ≥ 1 . Giá trị lớn nhất của biểu thức P=3x+4y-5 là với a, b là các số nguyên. Tính T = a 3 + b 3
A. 0
B. 250
C. 152
D. 98
