cho tam giác abc tia phân giác a cắt bc tại d tính đó đo góc adc biêt <b =75 độ <c =55 độ

Những câu hỏi liên quan
Cho tam giác ABC có B - C = 180 . Tia phân giác góc A cắt BC tại D . Tính số đo góc ADC ? góc ADB ?
Xét tam giác ABC: \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\Rightarrow\widehat{B}+\widehat{C}=180^0-\widehat{A}\)
Mặt khác: \(\widehat{B}-\widehat{C}=18^0\Rightarrow\left\{{}\begin{matrix}\widehat{B}=\dfrac{180^0-\widehat{A}+18^0}{2}=99^0-\dfrac{\widehat{A}}{2}\\\widehat{C}=99^0+\dfrac{\widehat{A}}{2}-18^0=81^0-\dfrac{\widehat{A}}{2}\end{matrix}\right.\)
Xét tam giác ABD: \(\widehat{ADC}=\widehat{BAD}+\widehat{B}=\dfrac{\widehat{A}}{2}+99^0-\dfrac{\widehat{A}}{2}=99^0\)
\(\widehat{ABD}=180^0-\widehat{ADC}=81^0\)
Đúng 0
Bình luận (0)
Cho tam giác ABC. Tia phân giác của góc A cắt BC tại D. Tính số đo
A
D
C
^
biết
B
^
-
C
^
20
o
A. 80
°
B. 110
°
C. 100
°
D. 105
°
Đọc tiếp
Cho tam giác ABC. Tia phân giác của góc A cắt BC tại D. Tính số đo A D C ^ biết B ^ - C ^ = 20 o
A. 80 °
B. 110 °
C. 100 °
D. 105 °
Cho tam giác ABC có góc B- góc C= 20 độ. Tia phân giác của góc A cắt BC tại D. Tính số đo của góc ADC, ADB
Cho tam giác ABC có góc B- góc C= 20 độ. Tia phân giác của góc A cắt BC tại D. Tính số đo của góc ADC, ADB
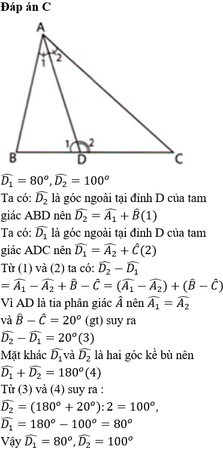
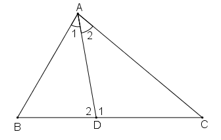
Trong ΔABD ta có ∠D1 là góc ngoài tại đỉnh D
∠D1 = ̂B + ∠A1 (tính chất góc ngoài của tam giác)
Trong ΔADC ta có ∠D2 là góc ngoài tại đỉnh D
∠D2 = ̂C + ∠A2 (tính chất góc ngoài của tam giác)
Ta có: ∠B > ∠C (gt); ∠A1 = ∠A2 (gt)
⇒∠D1 - ∠D2 = (B + ∠A1) - (C + ∠A2) = ∠B - ∠C = 20o
Lại có: ∠D1 + ∠D2 = 180o (hai góc kề bù)
⇒∠D1 = (180o + 20o):2 = 100o
⇒∠D1 = (100o - 20o) = 80o
Cho tam giác ABC có A= 80 độ ; B=70 độ. Tia phân giác của góc A cắt BC tại D ( D thuộc BC ).
a) tam giác ABD là tam giác gì? Vì sao?
b) Tính ADC, ACD
c) Tính số đo góc ngoài tại đỉnh B.
a) Xét tam giác ABC. Ta có:
Vì AD là tia phân giác của góc A nên:
\(\widehat{BAD}=\widehat{DAC}=\frac{\widehat{A}}{2}=40^{^o}\)
\(\widehat{ADB}=180^o-70^o-40^o=70^o\)
Vì \(\widehat{ADB}=\widehat{ABD}=70^o\)nên ABD là tam giác cân.
b)Vì \(\widehat{ADB}\)kề bù với \(\widehat{ADC}\)nên \(\widehat{ADC}=180^o-70^o=110^o\)
Do tam giác ACD là tam giác nên \(\widehat{ACD}=180^o-40^o-110^o=30^o\)
c) Đặt đỉnh ngoài của B là B1.
Ta có: \(\widehat{B_1}=180^o-70^o=110^o\)
Cho tam giác ABC có góc A=60o, góc B=80o, tia phân giác trong của góc A cắt BC tại D. Tính số đo góc ADC.
GT : \(\widehat{BAC}=60^o\); \(\widehat{B}=80^o\); \(\widehat{BAD}=\widehat{DAC}=\frac{\widehat{BAC}}{2}\)
KL : \(\widehat{ADC}=?\)
giải
vì AD là tia phân giác của \(\widehat{BAC}\)nên \(\widehat{BAD}=\widehat{DAC}=\frac{\widehat{BAC}}{2}=\frac{60^o}{2}=30^o\)
Vì \(\widehat{ADC}\)là góc ngoài của \(\Delta BAD\)nên \(\widehat{ADC}=\widehat{BAD}+\widehat{ABD}\)
hay \(\widehat{ADC}=80^o+30^o=110^o\)
Vậy \(\widehat{ADC}=110^o\)
Đúng 0
Bình luận (0)
Cho tam giác ABC tia phân giác của góc A cắt BC tại c tại d Tính góc ADC biết a,b=70
cho tam giác abc .co góc b-c= 20 độ .tia phân giác góc a cắt bc tại d .tính số đo của góc adc và adb
Cho tam giác ABC có góc B - C = 20 độ. Tia phân giác của góc A cắt Bc ở D. Tính số đo các góc ADC, ADB
Đặt \(\widehat{ADC}=b;\widehat{ADB}=a\)
Ta có: \(a+\widehat{B}+\widehat{BAD}=b+\widehat{C}+\widehat{CAD}\)
\(\Leftrightarrow a+\widehat{C}+20^0=b+\widehat{C}\)
\(\Leftrightarrow a-b=-20\)
mà a+b=180
nên 2a=160
=>a=80
=>b=100
Đúng 0
Bình luận (0)