Phương trình đường tròn (C) : (x + 1)² + (y - 3)² = 2 + 1 + 9 = 12

Vậy (C) có tâm A(-1 ; 3) và bán kính R = \(2\sqrt{3}\)

a, Phép đối xứng qua tâm O biết (C) thành một đường tròn có tâm có tọa độ là (1 ; -3) và bán kính vẫn bằng \(2\sqrt{3}\)

Phương trình đường tròn đó là : (x - 1)² + (y + 3)² = 12

b, Đối xứng qua tâm I (2 ; -3) biến A thành B và I là trung điểm của AB và bán kính đường tròn mới vẫn bằng \(2\sqrt{3}\). TÌm tọa độ I là được

Dễ thấy bán kính của (C') = 4. Tâm I của (C') là ảnh của tâm I(1;2) của (C) qua phép đồng dạng nói trên. Qua phép vị tự tâm O tỉ số k = -2 , I biến thành I 1 ( − 2 ;   − 4 ) . Qua phép đối xứng qua trục Ox, I 1  biến thành I′(−2;4).

Từ đó suy ra phương trình của (C') là x   +   2 2   +   y   −   4 2   =   16 .

Dễ thấy bán kính của (C') bằng 4. Tâm I' của (C') là ảnh của tâm I(1;2) của (C) qua phép đồng dạng nói trên. Qua phép vị tự tâm O, tỉ số \(k=-2,I\) biến thành \(I_1\left(-2;-4\right)\). Qua phép đối xứng qua trục \(Ox\), \(I_1\) biến thành \(I'\left(-2;4\right)\).

Từ đó suy ra phương trình của (C') là \(\left(x+2\right)^2+\left(y-4\right)^2=16\)

+ Gọi (I1; R1) là ảnh của (I; 2) qua phép vị tự tâm O, tỉ số 3.

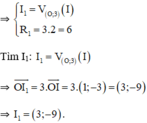
+ Gọi (I2; R2) là ảnh của (I1; R1) qua phép đối xứng trục Ox

⇒ R2 = R1 = 6.

I2 đối xứng với I1 qua Ox ⇒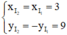 

⇒ I2(3; 9)

Vậy (I2; R2) chính là ảnh của (I; 2) qua phép đồng dạng trên và có phương trình: (x – 3)2 + (y – 9)2 = 36.

Đường tròn có pt:

\(\left(x-1\right)^2+\left(y-1\right)^2=8\)

Tâm \(I\left(1;1\right)\) và \(R=2\sqrt{2}\)

Gọi \(I_1\) là ảnh của I qua phép quay 

\(\Rightarrow\left\{{}\begin{matrix}x_{I1}=1.cos\left(-45^0\right)-1sin\left(-45^0\right)=\sqrt{2}\\y_{I_1}=1.sin\left(-45^0\right)+1.cos\left(-45^0\right)=0\end{matrix}\right.\)

\(\Rightarrow I_1\left(\sqrt{2};0\right)\)

Gọi \(I_2\) là ảnh của \(I_1\) qua phép vị tự:

\(\Rightarrow\left\{{}\begin{matrix}x_{I_2}=-\sqrt{2}.\sqrt{2}=-2\\y_{I_2}=-\sqrt{2}.0=0\end{matrix}\right.\) \(\Rightarrow I_2\left(-2;0\right)\)

\(R_2=\left|-\sqrt{2}\right|.2\sqrt{2}=4\)

Vậy pt đường tròn ảnh có dạng:

\(\left(x+2\right)^2+y^2=16\)

a. Phương trình đường tròn : (x – 3)2 + (y + 2)2 = 9.

b. (I1; R1) là ảnh của (I; 3) qua phép tịnh tiến theo vec tơ v.

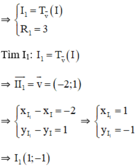
⇒ Phương trình đường tròn cần tìm: (x – 1)2 + ( y + 1)2 = 9.

c. (I2; R2) là ảnh của (I; 3) qua phép đối xứng trục Ox

⇒ R2 = 3 và I2 = ĐOx(I)

Tìm I2: I2 = ĐOx(I) ⇒ 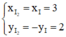 ⇒ I2(3; 2)

⇒ Phương trình đường tròn cần tìm: (x – 3)2 + (y – 2)2 = 9.

d. (I3; R3) là ảnh của (I; 3) qua phép đối xứng qua gốc O.

⇒ R3 = 3 và I3 = ĐO(I)

Tìm I3: I3 = ĐO(I) ⇒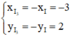 

⇒ Phương trình đường tròn cần tìm: (x + 3)² +(y – 2)² = 9.

Đáp án C

(C) có tâm I(1;2) bán kính  R = 3

Đ O : I → I’(–1;–2)

Phương trình đường tròn (C’): x + 1 2 + y + 2 2  = 3