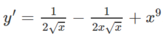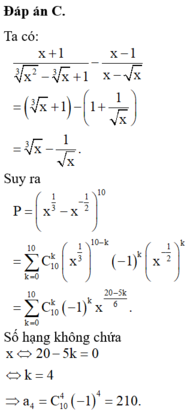x10 = 1x

Những câu hỏi liên quan
Tìm x
∈
N biết:a,
x
10
1
x
b,
x
10
x
c,
2
x
-
15...
Đọc tiếp
Tìm x ∈ N biết:
a, x 10 = 1 x
b, x 10 = x
c, 2 x - 15 5 = 2 x - 15 3
a) TH1: x = 0
x 10 = 1 x ⇔ 0 10 = 1 0
ó 0 = 1 vô lí => x = 0 không thỏa mãn.
TH2: x = 1
x 10 = 1 x ⇔ 1 10 = 1 1
ó 1 = 1 => x = 1 thỏa mãn.
TH3: x > 1
x 10 = 1 x ⇔ x 10 = 1
Mà x > 1 => x 10 > 1 => không có giá trị của x.
Vậy x = 1
b) Tương tự a). x = 0 hoặc x = 1.
c) Lũy thừa có cùng cơ số mà khác số mũ thì cơ số bằng 0 hoặc bằng 1.
TH1: Cơ số bằng 0.
=>2x – 15 = 0
ó x = 15 2 (do x ∈ N nên không thỏa mãn).
TH2: Cơ số bằng 1.
=>2x – 15 = 1
ó x = 8 (thỏa mãn)
Vậy x = 8.
Đúng 0
Bình luận (0)
Tìm
x
∈
N
biết:a)
x
10
1
x
b)
x
10
x
c)
(
2
x
-
15
)
5
(
2
x
-
15
)...
Đọc tiếp
Tìm x ∈ N biết:
a) x 10 = 1 x
b) x 10 = x
c) ( 2 x - 15 ) 5 = ( 2 x - 15 ) 3
Tìm đạo hàm của hàm số sau: y = x + 1 x + 0 , 1 . x 10
Tìm xϵN biết:
A)2x-15=17
B)(2x-11)5=24.32+99
C)x10=1x
a, 2\(^x\) - 15 = 17
2\(^x\) = 17 + 15
2\(^x\) = 32
2\(^x\) = 25
\(x\) = 5
b, (2\(x\) - 11)5 = 24.32 + 99
(2\(x\) - 11)5 = 16.9 + 99
(2\(x\) - 11)5 = 144 + 99
(2\(x\) - 11)5 = 243
(2\(x\) - 11)5 = 35
2\(x\) - 11 = 3
2\(x\) = 3 + 11
2\(x\) = 14
\(x\) = 14: 2
\(x\) = 7
c, \(x^{10}\) = 1\(^x\)
\(x^{10}\) = 1
\(x^{10}\) = 110
\(\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
\(x\) \(\in\) { -1; 1}
Đúng 2
Bình luận (0)
A) \(...\Rightarrow2^x=32=2^5\Rightarrow x=5\)
B) \(...\Rightarrow\left(2x-11\right)^5=243=3^5\)
\(\Rightarrow2x-11=5\Rightarrow2x=16\Rightarrow x=8\)
C) \(...\Rightarrow x^{10}=1=x^0\Rightarrow x=1\)
Đúng 0
Bình luận (0)
Tìm x:
a)(x-3)+(x-2)+(x-1)+...+10+11
b)x10=1x
Giúp mk vs
Tìm số hạng không chứa x trong khai triển nhị thức Newton của P:
P
x
+
1
x
2
3
−
x
+
1
3...
Đọc tiếp
Tìm số hạng không chứa x trong khai triển nhị thức Newton của P: P = x + 1 x 2 3 − x + 1 3 − x − 1 x − x 10 với x > 0 , x ≠ 1.
A. 200.
B. 100.
C. 210.
D. 160.
Cho biểu thức
P
x
+
1
x
2
3
-
x
+
1...
Đọc tiếp
Cho biểu thức P = x + 1 x 2 3 - x + 1 3 - x - 1 x - x 10 với x>0, x ≠ 1. Tìm số hạng không chứa x trong khai triển nhị thức Newton của P.
A. 200
B. 100
C. 210
D. 160
Bạn nào tính nhanh và chính xác mình sẽ cho một tick ( Lưu ý : Phải đầy đủ và chính xác, không viết luôn kết quả, viết phần kết quả ) :
Tính nhanh :
1x 5 x10 x 15 x 20 x....x 90 x 95 x 100
1x 5 x10 x 15 x 20 x....x 90 x 95 x 100
= 5x1x5x2x5x3x........5x20
= 5^21. 1.2.3.4.5.....20 = 5^21 x 1x2...x20
=...
Đúng 0
Bình luận (0)
TÍNH NHANH
10 x 10 x 10 x10 x 10 x 10 x 10 x10 x10 x10 = ?
Xem thêm câu trả lời