Cho hình vuông ABCD cạnh a.Gọi M là trung điểm của BC.Tính độ dài vecto AM + vecto BC

Những câu hỏi liên quan
cho hình thoi ABCD có góc A=60 độ,cạnh a.Gọi O là giao điểm của AC và BD.Tính độ dài vecto AB + vecto AD...vecto BA - vecto BC....vecto OB- vecto DC
cho hình chữ nhật ABCD ,AB =3 ;BC =4 .M,N là trung điểm của BC và CD .Tính a) độ dài vectoAB +vectoAC +vectoAD b)độ dài vecto AM +vecto AN
a: \(\left|\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AC}\right|=2\cdot AC=2\cdot5=10\)
b: \(\left|\overrightarrow{AM}+\overrightarrow{AN}\right|=\left|\dfrac{\overrightarrow{AB}+\overrightarrow{AC}}{2}+\dfrac{\overrightarrow{AD}+\overrightarrow{AC}}{2}\right|\)
\(=\left|\dfrac{3\cdot\overrightarrow{AC}}{2}\right|=\dfrac{3}{2}AC=\dfrac{3}{2}\cdot5=\dfrac{15}{2}=7.5\)
Đúng 0
Bình luận (0)
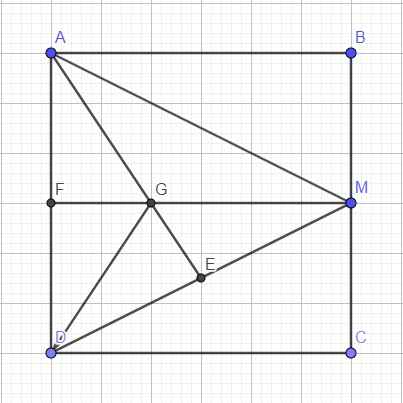
Cho hình vuông ABCD có độ dài cạnh bằng 6. Gọi M là trung điểm của BC và G là trọng tâm tam giác ADM. Tính độ dài vecto GD
\(\left\{{}\begin{matrix}AM=\sqrt{AB^2+BM^2}=3\sqrt{5}\\DM=\sqrt{CD^2+CM^2}=3\sqrt{5}\end{matrix}\right.\) \(\Rightarrow\) tam giác ADM cân tại M
Gọi F là trung điểm AD \(\Rightarrow ABMF\) là hình chữ nhật \(\Rightarrow MF=AB=6\)
Theo tính chất trọng tâm: \(GF=\dfrac{1}{3}MF=2\)
\(DF=\dfrac{1}{2}AD=3\)
Đặt \(T=\left|\overrightarrow{GD}\right|=\left|\overrightarrow{GF}+\overrightarrow{FD}\right|\)
\(\Rightarrow T^2=GF^2+FD^2+2\overrightarrow{GF}.\overrightarrow{DF}=GF^2+DF^2=2^2+3^2=13\)
\(\Rightarrow\left|\overrightarrow{GD}\right|=\sqrt{13}\)
Đúng 2
Bình luận (0)
Cho hình vuông cố định A,B,C,D cạnh a.Trên đường thẳng DC có điểm M thay đổi .Gọi K,E,J lần lượt là giao điểm của các cặp đường thẳng BC và AM,DK và DM,AM và CE .câu a,Tính Độ dài Vecto OJ,với O là tâm hình vuông ABCD.Câu b,Khi Vecto OJ cùng hướng với Vecto DC hãy tính độ dài vecto AM.Mọi người giải hộ mik nhé
cho hình vuông ABCD. I là trung điểm AD. N ∈ BC, CN = 2NB. Bt độ dài vecto IN =4. tìm độ dà vecto AC.
Cho hình vuông ABCD cạnh a.Gọi M là trung điểm BC.Tính \(\overrightarrow{AM}+\overrightarrow{AD}\) theo a
Lấy điểm F sao cho DF // AM và F thuộc BC
Theo quy tắc hình bình hành ( AM//DF ; AD //MF)
\(\overrightarrow{AF}=\overrightarrow{AD}+\overrightarrow{AM}\)
Vì AMFD là hình bình hành nên \(\left|\overrightarrow{AD}\right|=\left|\overrightarrow{MF}\right|\Rightarrow BF=\frac{a}{2}+a=\frac{3a}{2}\)
Theo định lý Pytago ta có:
\(\left|\overrightarrow{AF}\right|^2=a^2+\left(\frac{3a}{2}\right)^2=a^2+\frac{9a^2}{4}=\frac{13a^2}{4}\)
\(\Rightarrow\left|\overrightarrow{AF}\right|=\sqrt{\frac{13a^2}{4}}=\frac{a\sqrt{13}}{2}\)
Đúng 0
Bình luận (0)
Dễ tính được \(AM=\frac{\sqrt{5}a}{2}\)
Ta thấy M là trung điểm của BC tức \(MB=MC=\frac{1}{2}BC=\frac{1}{2}AB\Rightarrow\widehat{AMB}=60^0\)
\(AD//BC\Rightarrow\widehat{DAC}=\widehat{AMB}=60^0\)
\(\Rightarrow\overrightarrow{AD}+\overrightarrow{AM}=\sqrt{a^2+\frac{5a^2}{4}-2\cdot a\cdot\frac{\sqrt{5}a}{2}\cdot\cos120}\)
\(\Rightarrow\overrightarrow{AD}+\overrightarrow{AM}=\sqrt{\frac{9a^2}{4}+\frac{\sqrt{5}a^2}{2}}=\sqrt{\frac{9a^2+2\sqrt{5}a^2}{4}}=\frac{a}{2}\sqrt{9+2\sqrt{5}}\)
Chắc vậy ạ
Sai thì thông cảm mk nha
Đúng 0
Bình luận (0)
Cho hình vuông ABCD cạnh a, M là 1 điểm bất kỳ CMR các vecto ko phụ thuộc vào M và tính độ dài a, vecto MA +vecto MB-2vectoMF
Đề bài sai em
Điểm F là điểm nào nhỉ?
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD. Gọi M,N theo thứ tự là trung điểm của các cạnh BC,CD. Hãy biểu diễn các vecto BC,CD theo các vecto AM,AN
HD: \(\overrightarrow{BC}=\frac{-2}{3}\overrightarrow{AM}+\frac{4}{3}\overrightarrow{AN};\overrightarrow{CD}=\frac{-4}{3}\overrightarrow{AM}+\frac{2}{3}\overrightarrow{AN}\)
cho hình vuông abcd cạnh a d là đường thẳng đi qua a // bd . gọi m là điểm thuộc đường thẳng d sao cho |vecto ma + vecto mb + vecto mc - vecto md| nhỏ nhất .tính theo a độ dài vecto md