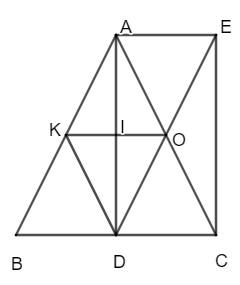
Cho tam giác ABC cân tại A, đường cao AD. O là trung điểm của AC, điểm E đối xứng với D qua O
a) Chứng minh tứ giác ADCE là hcn
b) Gọi I là trung điêm của AD, chứng minh AEDB là hbh
c) Cho AB= 10cm, BC= 12 cm . Tính S tam giác OAD
d) Đường thẳng OI cắt AB tại K. Tìm điều kiện của tam giác ABC để AE= DK