a: Xet ΔADB vuông tại D và ΔAEC vuông tại E có

góc A chung

=>ΔADB đồng dạng vơi ΔAEC

=>AD/AE=AB/AC
=>AD*AC=AE*AB; AD/AB=AE/AC

b: Xét ΔADE và ΔABC có

AD/AB=AE/AC

góc DAE chung

=>ΔADE đồng dạng với ΔABC

c: \(DB=\sqrt{5^2-3^2}=4\left(cm\right)\)

\(S_{BAC}=\dfrac{1}{2}\cdot4\cdot6=12\left(cm^2\right)\)

B1): a): +)Ta có csc đường cao BD, CE cắt nhau tại I => BD vg góc vs AC; CE vg góc vs AB

             +)Xét tg AEC và tg ADB, có: AEC=AHB=90( BD vg góc vs AC; CE vg góc vs AB )

                                                          BAC chung

                    Do đó: tg AEC ~ tg ADB ( gg)

         => AE/AD= AC/AB=> AE*AB=AD*AC (đpcm)

     b) : Gợi ý hoi :)): Kẻ đcao AF xuống BC, sẽ đi qua điểm I; c/m ED//BC=> c/m đc tg AED~tg ABC theo trường hợp cgc, từ đó ta sẽ có đc 2 góc AED = ABC ( vì 2 tg trên ~ vs nhau )

a, Vì BM là phân giác ^B nên : \(\frac{AB}{BC}=\frac{AM}{MC}\)( t/c )

\(\Rightarrow\frac{MC}{BC}=\frac{AM}{AB}\)( tỉ lệ thức )

Áp dụng tính chất dãy tỉ số bằng nhau ta có : 

\(\frac{MC}{BC}=\frac{AM}{AB}=\frac{MC+AM}{BC+AB}=\frac{5}{11}\)

\(\Rightarrow\frac{MC}{6}=\frac{5}{11}\Rightarrow MC=\frac{30}{11}\)cm 

\(\Rightarrow\frac{AM}{5}=\frac{5}{11}\Rightarrow AM=\frac{25}{11}\)cm

b, Vì MN // BC theo hệ quả Ta lét : 

\(\frac{MN}{BC}=\frac{AM}{AC}\Rightarrow MN=\frac{AM.BC}{AC}=\frac{\frac{25}{11}.6}{5}=\frac{30}{11}\)cm 

c, Ta có : \(\frac{\Delta_{AMN}}{\Delta_{ABC}}=\left(\frac{AM}{AB}\right)^2=\left(\frac{25}{\frac{11}{5}}\right)^2=\frac{25}{121}\)

d, Ko có H :> 

a) xét \(\Delta ADB\)zà \(\Delta AEC\)có

\(\hept{\begin{cases}\widehat{A}chung\\\widehat{AEC}=\widehat{ADB}=90^0\end{cases}}\)

\(=>\Delta ADB~\Delta AEC\left(g.g\right)\)

\(=>\frac{AD}{AE}=\frac{AB}{AC}=>AD.AC=AB.AE\left(dpcm\right)\)

\(taco\left(\frac{AD}{AE}=\frac{AB}{AC}=>\frac{AD}{AB}=\frac{AE}{AC}\right)\)

xét \(\Delta ADE\)zà \(\Delta ABCco\)

\(\hept{\begin{cases}\widehat{A}chung\\\frac{AD}{AB}=\frac{AE}{AC}\end{cases}=>\Delta ABE~\Delta ABC\left(c.g.c\right)}\)

=>\(\widehat{ADE}=\widehat{ABC}\left(dpcm\right)\)

c) Xét tam giác AEC zà tam giác HDC óc

góc AEC= góc HDC =90 độ

góc HCE chung

=> tam giác AEC~ tam giác HDC 

=>\(\frac{AC}{HC}=\frac{EC}{DC}=>AC.DC=EC.HC\left(1\right)\)

xét tam giác BEC zà tam giác HEA có

góc BEC= góc AEH= 90 độ

góc BCE = góc  EAH ( cùng phụ zới góc EBC )

=> tam giác BEC ~ tam giác HEA (g.g)

=>\(\frac{BE}{HE}=\frac{EC}{EA}=>BE.EA=EC.HE\left(2\right)\)

từ 1 zà 2 suy ra

\(BE.BA+CD.CA=BH.BD+CH.CE\)

kẻ AH zuông goc zới BC cắt BC tại F

Tự CM \(\hept{\begin{cases}\Delta CFH~\Delta CEB\\\Delta BFH~\Delta BDC\end{cases}=>\hept{\begin{cases}CF.CB=CH.CE\\BF.BC=BH.BD\end{cases}=>BE.BA+CD.CA=CF.CB+BF.CB}}\)

\(=BC.\left(CF+BF\right)=BC^2\)

b) Theo câu a ta có

\(\widehat{ADE}=\widehat{ABC}\)

mà \(\hept{\begin{cases}\widehat{ADE}+\widehat{EDH}=90^0\\\widehat{EBC}+\widehat{BCE}=90^0\end{cases}=>\widehat{EDH}=\widehat{ECB}}\)

xét tam giác EHD zà tam giác HBC có

góc EHD= góc BHC

góc EDH = góc HCB

=> ttam giác EHD ~ tam giác HBC

a: Xét ΔABC có

BD là đường cao ứng với cạnh AC

CE là đường cao ứng với cạnh AB

BD cắt CE tại H 

Do đó: H là trực tâm của ΔBAC

hay AH\(\perp\)BC tại K

Xét ΔBKH vuông tại K và ΔBDC vuông tại D có

\(\widehat{HBK}\) chung

Do đó: ΔBKH\(\sim\)ΔBDC

Suy ra: \(\dfrac{BK}{BD}=\dfrac{BH}{BC}\)

hay \(BH\cdot BD=BK\cdot BC\)

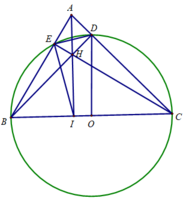
d) Tính BE.BA + CD.CA

Chứng minh tương tự câu b, CD.CA = CI.CB

Từ đó BE.BA + CD.CA = BI.BC + CI.CB

= (BI + CI).BC = BC.BC = B C 2 = 16 2  = 256

a) Xét ΔAHE vuông tại E và ΔABD vuông tại D có 

\(\widehat{EAH}\) chung

Do đó: ΔAHE\(\sim\)ΔABD(g-g)

Suy ra: \(\dfrac{AH}{AB}=\dfrac{AE}{AD}\)

hay \(AB\cdot AE=AH\cdot AD\)

b) Xét ΔEHA vuông tại E và ΔEBC vuông tại E có 

\(\widehat{AHE}=\widehat{CBE}\)(ΔAHE\(\sim\)ΔABD)

Do đó: ΔEHA\(\sim\)ΔEBC(g-g)

Suy ra: \(\dfrac{EH}{EB}=\dfrac{EA}{EC}\)

hay \(EA\cdot EB=EH\cdot EC\)

d) Ta có: ΔABC cân tại A(gt)

mà AD là đường cao ứng với cạnh đáy BC(Gt)

nên AD là đường trung tuyến ứng với cạnh BC

Suy ra: \(BD=DC=\dfrac{BC}{2}=\dfrac{6}{2}=3\left(cm\right)\)

Áp dụng định lí Pytago vào ΔABD vuông tại D, ta được:

\(AD^2+BD^2=AB^2\)

\(\Leftrightarrow AD^2=5^2-3^2=16\)

hay AD=4(cm)

Xét ΔBEC vuông tại E và ΔBDA vuông tại D có 

\(\widehat{B}\) chung

Do đó: ΔBEC\(\sim\)ΔBDA(g-g)

Suy ra: \(\dfrac{BE}{BD}=\dfrac{BC}{BA}\)

\(\Leftrightarrow BE=\dfrac{6\cdot3}{5}=\dfrac{18}{5}=3.6\left(cm\right)\)

Áp dụng định lí Pytago vào ΔBEC vuông tại E, ta được:

\(BC^2=BE^2+EC^2\)

\(\Leftrightarrow EC^2=6^2-3.6^2=23.04\)

hay EC=4,8(cm)