Cho hình vẽ chứng minh rằng BD + CE < AB + AC

Những câu hỏi liên quan
Cho hình vẽ chứng minh rằng BD + CE <AB + AC giải giúp mình nha ! Vẽ hình giúp mình luôn nha
1.cho tam giác ABC (ABAC) .Vẽ BD vuông góc với AC và CE vuông góc với AB tại E . Chứng minh rằng AB - ADBD - CE2.cho tam giác ABC(ABAC) , vẽ BD vuông góc với AC tại D và CE vuông góc với AB tại E . Chứng minh rằng : AB - AD BD -CE3.cho tam giác ABC cân tại A , trên 2 cạnh AB AB và AC lấy 2 điểm M và N sao cho AM AN . Chứng minh rằnga)Các hình chiếu của BM và CN trên BC bằng nhau b) BN (BC+MN)/2bài 3 giải giúp mik câu b thoy
Đọc tiếp
1.cho tam giác ABC (AB<AC) .Vẽ BD vuông góc với AC và CE vuông góc với AB tại E . Chứng minh rằng AB - AD>BD - CE
2.cho tam giác ABC(AB>AC) , vẽ BD vuông góc với AC tại D và CE vuông góc với AB tại E . Chứng minh rằng : AB - AD > BD -CE
3.cho tam giác ABC cân tại A , trên 2 cạnh AB AB và AC lấy 2 điểm M và N sao cho AM =AN . Chứng minh rằng
a)Các hình chiếu của BM và CN trên BC bằng nhau
b) BN > (BC+MN)/2
bài 3 giải giúp mik câu b thoy
3b)
Ta có tg BNK vuông tại K ->BN>BK
Ta có IK=MN(tính chất đoạn chắn)
Ta có : BC+MN=BK+KC+MN=BK+BI+IK=2BK
Vì BK<BN->2BK<2BN->BN>BK/2->BN>BC+MN/2
Đúng 0
Bình luận (0)
Bài 5. Cho tam giác ABC nhọn, 𝐵̂>𝐶̂, đường cao BD và CE. Trên AC lấy điểm M sao cho AM = AB. Vẽ MN vuông góc AB, MF vuông góc CE
a) Chứng minh rằng: MN = EF
b) Chứng mịnh rằng: CM = AC - AB
c) Chứng minh rằng: AC – AB > CE – BD.
Bài 5. Cho tam giác ABC nhọn, 𝐵̂>𝐶̂, đường cao BD và CE. Trên AC lấy điểm M sao cho AM = AB. Vẽ MN vuông góc AB, MF vuông góc CE
a) Chứng minh rằng: MN = EF
b) Chứng mịnh rằng: CM = AC - AB
c) Chứng minh rằng: AC – AB > CE – BD.
Cho tam giác ABC có AB = AC ( góc A < 90o). Kẻ BD vuông góc với AC (D thuộc AC). Kẻ CE vuông góc với AB ( E thuộc AB). Chứng minh rằng BD = CE
AI VẼ HÌNH MÌNH TICK CHO NHA
Tam giác ABC cân tại A => AB=AC
=> góc ABC=ACB
Xét tam giác ECB và tam giác DBC có:
BC chung
góc BEC=CDB = 90 độ
góc EBC=DCB
=> tam giác ECB = tam giác DBC ( cạnh huyền-góc nhọn)
=> BD=CE ( 2 cạnh tương ứng)
Bài 1. Cho ABC cân tại A. Kẻ BD AC, CE AB (D AC; E AB). Gọi I là giao điểm BD và CE. Chứng minh rằng:
a) BE = CD
b) AI là phân giác BAC
c) Vẽ AK BC tại K. Chứng minh rằng AK, BD, CE cùng đi qua một điểm.
a: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó:ΔEBC=ΔDCB
Suy ra: BE=CD
b: Ta có: ΔEBC=ΔDCB
nên \(\widehat{ECB}=\widehat{DBC}\)
hay ΔIBC cân tại I
Ta có: AE+EB=AB
AD+DC=AC
mà AB=AC
và EB=DC
nên AE=AD
Xét ΔABI và ΔACI có
AB=AC
AI chung
BI=CI
Do đó: ΔABI=ΔACI
Suy ra: \(\widehat{BAI}=\widehat{CAI}\)
hay AI là tia phân giác của góc BAC
c: Xét ΔABC có
BD là đường cao
CE là đường cao
BD cắt CE tại I
Do đó: I là trực tâm của ΔABC
Suy ra: AI\(\perp\)BC
mà AK\(\perp\)BC
nên A,I,K thẳng hàng
=>AK,BD,CE đồng quy
Đúng 0
Bình luận (0)
Cho hình sau, chứng minh rằng: BD + CE < AB + AC
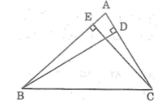
Trong ΔABD, ta có ∠(ADB) = 90o
Suy ra: BD < AB (đường vuông góc ngắn hơn đường xiên) (1)
Trong ΔAEC, ta có ∠(AEC) = 90o
Suy ra: CE < AC (cạnh huyền lớn hơn cạnh góc vuông) (2)
Cộng từng vế (1) và (2), ta có: BD + CE < AB + AC.
Đúng 0
Bình luận (0)
cho tam giác ABC, AB >AC . Vẽ BD vuông góc với AC , , CE vuông góc với AB ( D thuộc AC, E thuộc AB ) Chứng minh rằng : AB - AC > BD - CE
1 ) Cho tam giác cân ABC . Vẽ AH ⊥ BC tại H . Chứng minh rằng :
a ) AH là tia phân giác của góc A
b ) HB = HC
2 ) Cho tam giác ABC cân tại A . Vẽ BD ⊥ AC , CE ⊥ AB . Chứng minh rằng : BD = CE
Bạn tự vẽ hình nha
1. a) ta có: tg abc cân => AB=AC; AH vừa là trung tuyến vừa là phân giác của tg abc (1)
=> AH là tia phân giác của góc A
b) từ (1) => AH là trung tuyến của tg abc
=> HB=HC
2. ta có: tg abc cân; ab=ac
=> bd và ce vừa là đường cao vừa là trung tuyến của tg abc
=> ad=dc; ab=be ( mà ab=ac)
=> ae=ad
tg abd= tg ace: ab=ac; góc a chung; ae=ad
=> bd=ce
học tốt nha bạn
Đúng 0
Bình luận (0)













