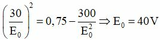1.theat...e
2.kara...e
3.pat...ent
4.sm...rt
5.dent...st
6.no...sy
7.eng...neer
8.br...dge
Những câu hỏi liên quan
Giả sử trong ô E2 chứa công thức =(B2+D2)*A2 . Hãy cho biết kết quả ở ô E3 của thao tác sau:
a) Di chuyển nội dung công thức trong ô E2 sang ô E3?
b) Sao chép nội dung công thức trong ô E2 sang ô E3?
a) Kết quả sau khi di chuyển là: =(B3+D3)*A3
b) Kết quả sau khi sao chép là: =(B3+D3)*A3
Một máy phát điện xoay chiều ba pha đang hoạt động ổn định. Suất điện động trong ba cuộn dây của phần ứng có giá trị
e
1
,
e
2
,
e
3
. Ở thời điểm mà
e
1
30
V
thì ...
Đọc tiếp
Một máy phát điện xoay chiều ba pha đang hoạt động ổn định. Suất điện động trong ba cuộn dây của phần ứng có giá trị e 1 , e 2 , e 3 . Ở thời điểm mà e 1 = 30 V thì e 2 - e 3 = 30 V. Giá trị cực đại của e 1 là:
A. 40,2 V
B. 51,9 V
C. 34,6 V
D. 45,1V.
Một máy phát điện xoay chiều ba pha đang hoạt động ổn định. Suất điện động trong ba cuộn dây của phần ứng có giá trị e1, e2 và e3. Ở thời điểm mà e1 30V thì |e2 – e3| 30V. Giá trị cực đại của e1 là A. 40,2 V B. 51,9V C. 34,6 V D. 45,1 V
Đọc tiếp
Một máy phát điện xoay chiều ba pha đang hoạt động ổn định. Suất điện động trong ba cuộn dây của phần ứng có giá trị e1, e2 và e3. Ở thời điểm mà e1 = 30V thì |e2 – e3| = 30V. Giá trị cực đại của e1 là
A. 40,2 V
B. 51,9V
C. 34,6 V
D. 45,1 V
Một máy phát điện xoay chiều ba pha đang hoạt động ổn định. Suất điện động trong ba cuộn dây của phần ứng có giá trị
e
1
,
e
2
và
e
3
. Ở thời điểm mà
e
1
30
V
thì
e
2
−...
Đọc tiếp
Một máy phát điện xoay chiều ba pha đang hoạt động ổn định. Suất điện động trong ba cuộn dây của phần ứng có giá trị e 1 , e 2 và e 3 . Ở thời điểm mà e 1 = 30 V thì e 2 − e 3 = 30 V . Giá trị cực đại của e 1 là:
A. 40,2 V
B. 51,9 V
C. 34,6 V
D. 45,1V
Một máy phát điện xoay chiều ba pha đang hoạt động ổn định. Suất điện động trong ba cuộn dây của phần ứng có giá trị
e
1
,
e
2
,
e
3
. Ở thời điểm mà
e
1
30 V thì
e
2
-
e
3...
Đọc tiếp
Một máy phát điện xoay chiều ba pha đang hoạt động ổn định. Suất điện động trong ba cuộn dây của phần ứng có giá trị e 1 , e 2 , e 3 . Ở thời điểm mà e 1 = 30 V thì e 2 - e 3 = 30 V . Giá trị cực đại của e 1 là
A. 40,2 V
B. 51,9V
C. 34,6 V
D. 45,1 V
Một máy phát điện xoay chiều ba pha đang hoạt động ổn định. Suất điện động trong ba cuộn dây của phần ứng có giá trị
e
1
,
e
2
và
e
3
. Ở thời điểm mà
e
1
30
V
thì
e
2
−
e...
Đọc tiếp
Một máy phát điện xoay chiều ba pha đang hoạt động ổn định. Suất điện động trong ba cuộn dây của phần ứng có giá trị e 1 , e 2 và e 3 . Ở thời điểm mà e 1 = 30 V thì e 2 − e 3 = 30 V . Giá trị cực đại của e 1 là
A. 40,2 V
B. 51,9 V
C. 34,6 V
D. 45,1 V
Chọn đáp án C.
Giả sử ở thời điểm t nào đó ta có như trên VTLG
Giả sử suất điện động xuất hiện trong khung dây có dạng e 1 = E 0 cos ω t 1 e 2 = E 0 cos ω t + 2 π 3 e 3 = E 0 cos ω t − 2 π 3 (1)
e 2 = E 0 cos ω t + 2 π 3 e 3 = E 0 cos ω t − 2 π 3 → e 2 - e 1 = ± 30 E 0 cos ω t + 2 π 3 − cos ω t − 2 π 3 = ± 30 ( 2 )
Áp dụng công thức toán học cos a − cos b = − 2 sin a + b 2 sin a − b 2
Phương trình (2) được viết lại: − 2 E 0 sin ω t sin 2 π 3 = ± 30 . Kết hợp với (1) ta có:
− 2 E 0 sin ω t sin 2 π 3 = ± 30 e 1 = E 0 cos ω t = 30 ⇔ E 0 sin ω t = ± 10 3 E 0 cos ω t = 30 ⇒ E 0 ± 10 3 2 + E 0 30 2 = 1 ⇒ E 0 = 20 3 ≈ 34 , 6 V
Đúng 0
Bình luận (0)
Một máy phát điện xoay chiều ba pha đang hoạt động ổn định. Suất điện động trong ba cuộn dây của phần ứng có giá trị
e
1
,
e
2
và
e
3
. Ở thời điểm mà
e
1
30
V
thì
e
2
-
e...
Đọc tiếp
Một máy phát điện xoay chiều ba pha đang hoạt động ổn định. Suất điện động trong ba cuộn dây của phần ứng có giá trị e 1 , e 2 và e 3 . Ở thời điểm mà e 1 = 30 V thì e 2 - e 3 = 30 V . Giá trị cực đại của e 1 là
A. 40,2 V
B. 51,9V
C. 34,6 V
D. 45,1 V
Tại ô E2 có công thức =B2+C2, thực hiện sao chép công thức sang ô E3. Công thức tại ô E3 sẽ là
A.=C3+D3
B.=C2+D2
C.=A2+B2
D.=B3+C3
Một máy phát điện xoay chiều ba pha đang hoạt động ổn định. Suất điện động trong ba cuộn dây của phần ứng có giá trị el, e2 và e3. Ở thời điểm mà e1 30 V thì│e2 - e3│ 30 V. Giá trị cực đại của e1 là A. 40,2 V. B. 51,9V. C. 34,6 V. D. 45,1 V.
Đọc tiếp
Một máy phát điện xoay chiều ba pha đang hoạt động ổn định. Suất điện động trong ba cuộn dây của phần ứng có giá trị el, e2 và e3. Ở thời điểm mà e1 = 30 V thì│e2 - e3│= 30 V. Giá trị cực đại của e1 là
A. 40,2 V.
B. 51,9V.
C. 34,6 V.
D. 45,1 V.
Giải thích: Đáp án C
Giả sử ở thời điểm t nào đó ta có như trên VTLG
Giả sử suất điện động xuất hiện trong khung dây có dạng
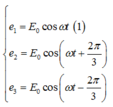
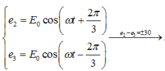
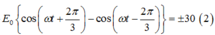
Áp dụng công thức toán học 
Phương trình (2) được viết lại:
. Kết hợp với (1) ta có
Đúng 0
Bình luận (0)
Một máy phát điện xoay chiều ba pha đang hoạt động bình thường. Trong ba cuộn dây của phần ứng có ba suất điện động có giá trị
e
1
,
e
2
,
e
3
. Ở thời điểm mà
e
1...
Đọc tiếp
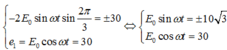
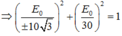
Một máy phát điện xoay chiều ba pha đang hoạt động bình thường. Trong ba cuộn dây của phần ứng có ba suất điện động có giá trị e 1 , e 2 , e 3 . Ở thời điểm mà e 1 = 30 V thì tích e 2 . e 3 = - 300 . Giá trị cực đại của e 1 là:
A. 50 V
B. 40 V
C. 45 V
D. 35 V
Đáp án B
+ Ta có: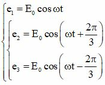 
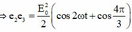
+ Theo đề 
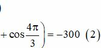
+ Biến đổi (2) ta co
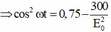(3)
+ Từ (1) và (3) ta có:
Đúng 0
Bình luận (0)