Giải giúp em câu này với câu c giải chi tiết xíu ạ

Những câu hỏi liên quan
Giải giúp mình bài này với ạ giải câu c chi tiết xíu giúp mình với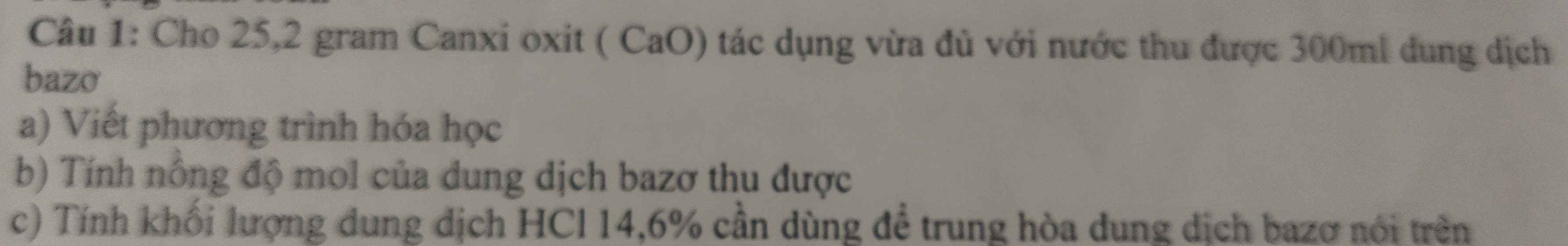
Giải chi tiết mấy câu này giúp em với ạ
24.
Đường thẳng có 1 vtcp là \(\overrightarrow{u}=\left(2;-5\right)\)
25.
\(a^2=b^2+c^2-2bc.cosA\)
26.
A là mệnh đề sai, công thức đúng: \(S=\dfrac{1}{2}ab.sinC\)
27.
\(BC=\sqrt{AB^2+AC^2-2AB.AC.cosA}=\sqrt{3^2+4^2-2.3.4.cos60^0}=\sqrt{13}\)
28.
\(\widehat{A}=180^0-\left(35^030'+45^0\right)=99^030'\)
Áp dụng định lý hàm sin:
\(\dfrac{a}{sinA}=\dfrac{b}{sinB}\Rightarrow b=\dfrac{a.sinB}{sinA}=\dfrac{12,5.sin\left(35^030'\right)}{sin\left(99^030'\right)}=7,36\left(m\right)\)
Đúng 2
Bình luận (0)
Mọi người giúp em giải chi tiết 2 câu này với ạ

mọi người giúp em giải chi tiết câu này với ạ 😿
theo mình thì câu trên: dưới mẫu trong căn bỏ n^2 ra làm nhân tử chung xong đặt nhân tử chung của cả mẫu là n^2 . câu dưới thì mình k biết!!
Đúng 0
Bình luận (0)
\(\lim\dfrac{-3n+2}{n-\sqrt{4n+n^2}}=\lim\dfrac{\left(-3n+2\right)\left(n+\sqrt{4n+n^2}\right)}{\left(n-\sqrt{4n+n^2}\right)\left(n+\sqrt{4n+n^2}\right)}\)
\(=\lim\dfrac{\left(-3n+2\right)\left(n+\sqrt{4n+n^2}\right)}{-4n}=\lim\dfrac{n\left(-3+\dfrac{2}{n}\right)n\left(1+\sqrt{\dfrac{4}{n}+1}\right)}{-4n}\)
\(=\lim n\dfrac{\left(-3+\dfrac{2}{n}\right)\left(1+\sqrt{\dfrac{4}{n}+1}\right)}{-4}\)
Do \(\lim\left(n\right)=+\infty\)
\(\lim\dfrac{\left(-3+\dfrac{2}{n}\right)\left(1+\sqrt{\dfrac{4}{n}+1}\right)}{-4}=\dfrac{\left(-3+0\right)\left(1+\sqrt{0+1}\right)}{-4}=\dfrac{3}{2}>0\)
\(\Rightarrow\lim n\dfrac{\left(-3+\dfrac{2}{n}\right)\left(1+\sqrt{\dfrac{4}{n}+1}\right)}{-4}=+\infty\)
Đúng 0
Bình luận (0)
\(\lim\left(\sqrt[3]{n^3+9n^2}-n\right)=\lim\dfrac{\left(\sqrt[3]{n^3+9n^2}-n\right)\left(\sqrt[3]{\left(n^3+9n^2\right)^2}+n\sqrt[3]{n^3+9n^2}+n^2\right)}{\sqrt[3]{\left(n^3+9n^2\right)}+n\sqrt[3]{n^3+9n^2}+n^2}\)
\(=\lim\dfrac{9n^2}{\sqrt[3]{\left(n^3+9n^2\right)^2}+n\sqrt[3]{n^3+9n^2}+n^2}\)
\(=\lim\dfrac{9n^2}{n^2\sqrt[3]{\left(1+\dfrac{9}{n}\right)^2}+n^2\sqrt[3]{1+\dfrac{9}{n}}+n^2}\)
\(=\lim\dfrac{9}{\sqrt[3]{\left(1+\dfrac{9}{n}\right)^2}+\sqrt[3]{1+\dfrac{9}{n}}+1}\)
\(=\dfrac{9}{\sqrt[3]{\left(1+0\right)^2}+\sqrt[3]{1+0}+1}=\dfrac{9}{3}=3\)
Đúng 0
Bình luận (0)
Giải giúp em chi tiết câu này ạ
Em cảm ơn
Mọi người ơi giúp em với 2 câu này đc ko ạ (giải chi tiết cho em nha, em cảm ơn nhiều ạ)

10.
\(H\left(x\right)=-5x^4+10x^3-15x+1\)
\(=-5x\left(x^3-2x^2+3\right)+1\)
\(=-5x.0+1\)
\(=1\)
9.
\(P\left(x\right)-Q\left(x\right)=\left(1-a\right)x^3+x^2+x-6\)
\(P\left(x\right)-Q\left(x\right)\) là đa thức bậc 3 khi và chỉ khi \(1-a\ne0\)
\(\Rightarrow a\ne1\)
Đúng 2
Bình luận (0)
Giúp em với mn, câu c thôi ạ. Giải chi tiết (ko tắt) hộ em với ạ

a: Thay \(x=3+2\sqrt{2}\) vào A, ta được:
\(A=\dfrac{3+2\sqrt{2}-\sqrt{2}-1+2}{\sqrt{2}+1+3}=\dfrac{4+\sqrt{2}}{4+\sqrt{2}}=1\)
Đúng 1
Bình luận (0)
\(b,B=\dfrac{x-4+2\sqrt{x}+6-3\sqrt{x}-4}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\\ B=\dfrac{x-\sqrt{x}+2}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\\ c,M=B:A=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\cdot\dfrac{\sqrt{x}+3}{x-\sqrt{x}+2}=\dfrac{\sqrt{x}+1}{x-\sqrt{x}+2}\\ M=\dfrac{x-\sqrt{x}+2-x+2\sqrt{x}-1}{x-\sqrt{x}+2}\\ M=1-\dfrac{x-2\sqrt{x}+1}{x-\sqrt{x}+2}=1-\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\)
Ta có \(\left(\sqrt{x}-1\right)^2\ge0;x-\sqrt{x}+2=\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{7}{4}>0\)
Do đó \(\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\ge0\)
\(\Leftrightarrow M=1-\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\le1-0=1\)
Vậy \(M_{max}=1\Leftrightarrow\sqrt{x}=1\Leftrightarrow x=1\left(tm\right)\)
Đúng 0
Bình luận (0)
Giải chi tiết câu này giúp mik với ạ ;-;
Phương trình đường tròn (C):
\(\left(x-1\right)^2+\left(y-2\right)^2=3^2\)
\(\Leftrightarrow\left(x-1\right)^2+\left(y-2\right)^2=9\)
Đúng 5
Bình luận (0)
Giải chi tiết câu này giúp mik với ạ ;-;
Đường tròn (C) viết lại: \(\left(x-0\right)^2+\left(y-0\right)^2=3^2\)
Do đó đường tròn có tâm \(I\left(0;0\right)\) và bán kính \(R=3\)
Đúng 1
Bình luận (0)
Giải chi tiết câu này giúp mik với ạ ;-;
\(\left(x-1\right)^2+\left(y+2\right)^2=25\)
\(\Leftrightarrow x^2-2x+1+y^2+4y+4=25\)
\(\Leftrightarrow x^2+y^2-2x+4y-20=0\)
Đúng 5
Bình luận (0)
















