trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD có đỉnh A(-1,2) và tâm I(1/2:0) xác định tọa độ các đỉnh còn lại của hình chữ nhật ABCD, biết đường thẳng BC đi qua điểm m(4;-3)
I là trung điểm AC \(\Rightarrow C\left(2;-2\right)\)
\(\Rightarrow\overrightarrow{CM}=\left(2;-1\right)\Rightarrow\) đường thẳng BC có dạng:
\(1\left(x-2\right)+2\left(y+2\right)=0\Leftrightarrow x+2y+2=0\)
Đường thẳng AB qua A và vuông góc BC nên nhận \(\left(2;-1\right)\) là 1 vtpt
Phương trình AB:
\(2\left(x+1\right)-1\left(y-2\right)=0\Leftrightarrow2x-y+4=0\)
B là giao điểm AB và BC nên tọa độ là nghiệm:
\(\left\{{}\begin{matrix}x+2y+2=0\\2x-y+4=0\end{matrix}\right.\) \(\Rightarrow B\left(...\right)\)
I là trung điểm BD \(\Rightarrow\left\{{}\begin{matrix}x_D=2x_I-x_B=...\\y_D=2y_I-y_B=...\end{matrix}\right.\)
Cho hình chữ nhặt ABCD có AD=3AB. Lấy điểm M trên cạnh BC. Đường thẳng AM cắt đường thẳng CD tại P. Đường thẳng EF ⊥ AM cắt AB tại E và CD tại F. Đường phân giác của góc DAM cắt CD tại K. CMR: a) EF=3BM+DKEF=3BM+DK b) 1/AB^2=1/AM^2+9/AP^2
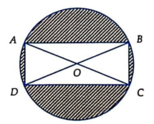
Một mảnh vườn hình chữ nhật có diện tích 961 m 2 , người ta muốn mở rộng thêm 4 phần đất sao cho tạo thành hình tròn ngoại tiếp mảnh vườn. Biết tâm hình tròn trùng với tâm hình chữ nhật. Tính diện tích nhỏ nhất của 4 phần đất được mở rộng
A. 961 π − 961 m 2
B. 1922 π − 961 m 2
C. 1892 π − 961 m 2
D. 480 , 5 π − 961 m 2
Một mảnh vườn hình chữ nhật có diện tích 961m2, người ta muốn mở rộng thêm 4 phần đất sao cho tạo thành hình tròn ngoại tiếp mảnh vườn. Biết tâm hình tròn trùng với tâm hình chữ nhật. Tính diện tích nhỏ nhất của 4 phần đất được mở rộng.
A. 961 π - 961 m 2
B. 1922 π - 961 m 2
C. 1892 π - 961 m 2
D. 480 , 5 π - 961 m 2
Đáp án D
Gọi x,y (m) lần lượt là hai kích thước của mảnh vườn x > 0 , y > 0
R(m) là bán kính đường tròn ngoại tiếp mảnh vườn ⇒ R 2 = O B 2 = x 2 4 + y 2 4
Theo đề bài x y = 961 m 2
Diện tích 4 phần đất mở rộng là:
S = S t r o n - S A B C D = πR 2 - xy = π . x 2 + y 2 4 - xy ≥ π 2 xy 4 - xy = 480 , 5 π - 961
cho hình chữ nhật ABCD AD<AB<2AD vẽ tam giác ABI, CDK vào trong hình chữ nhật I=K=90 E,K lần lượt là giao điểm của AI,DK và CK,CI .a chứng minh EF//CD b tứ giác EKFI là hình vuôngcho hình chữ nhật ABCD AD<AB<2AD vẽ tam giác ABI, CDK vào trong hình chữ nhật I=K=90 E,K lần lượt là giao điểm của AI,DK và CK,CI .a chứng minh EF//CD b tứ giác EKFI là hình vuông
cho hình vẽ ABCD là hình chữ nhật . AB = 4 cm các đường trong tâm A và tâm D cùng bán kính r= AB cắt cạnh AD tại G và E.
a)so sánh diện tích hình 1 và 2 neeud biết diện tích hình chữ nhật băng nửa diện tích tích hình tròn tâm A bán kính r
b) tính độ dài đoạn BG
k cho mình rồi mình gửi cho
Trong hệ tọa độ Oxy, cho hình chữ nhật ABCD có A(0; 3); D(2; 1) và I(-1 ; 0) là tâm của hình chữ nhật. Tìm tọa độ tung điểm của cạnh BC
A. (1 ; 2)
B. (-2; -3)
C. (-3 ; -2)
D. (- 4 ; -1)
Gọi M là tọa độ trung điểm của cạnh AD => M (1 ; 2)
Gọi N ( x N ; y N ) là tọa độ trung điểm của cạnh BC
Do I là tâm của hình chữ nhật nên I là trung điểm của MN.
Suy ra
x N = 2 x I − x M = − 3 y N = 2 y I − y M = − 2 ⇒ N − 3 ; − 2 .
Đáp án C
Trong hệ tọa độ Oxy, cho hình chữ nhật ABCD có A(0 ; 3) ; D(2 ; 1) và I( -1 ; 0) là tâm của hình chữ nhật. Tìm tọa độ tung điểm của cạnh BC.
A. (1; 2)
B. (-2; -3)
C. (-3; -2)
D. (-4; -1)
Gọi M là tọa độ trung điểm của cạnh AD => M (1 ; 2).
Gọi N ( x N ; y N ) là tọa độ trung điểm của cạnh BC.
Do I là tâm của hình chữ nhật nên I là trung điểm của MN.
Suy ra x N = 2 x I − x M = − 3 y N = 2 y I − y M = − 2 ⇒ N − 3 ; − 2 .
Đáp án C
Cho hình chữ nhật ABCD trên cạnh AB lấy điểm E sao cho ae = 1/4 AB EC cắt BD tại K me với d a tìm tỉ số diện tích tam giác aed và tam giác EBC b Biết diện tích tam giác DK diện tích tam giác AKB là 3 cm². tính diện tích hình chữ nhật ABCD
Cho tam giác ABC (AB<AC), đường cao AK. Gọi D; E; F theo thứ tự là trung điểm của AB; BC; AC.
a. Tứ giác ADEF là hình gì?
b. Tam giác ABC có điều kiện gì thì tứ giác ADEF là hình chữ nhật?
c. Chứng minh tứ giác DKEF là hình thang cân.
d. Cho BK = 6cm; AB = 10cm. Tính diện tích tam giác ABK?
