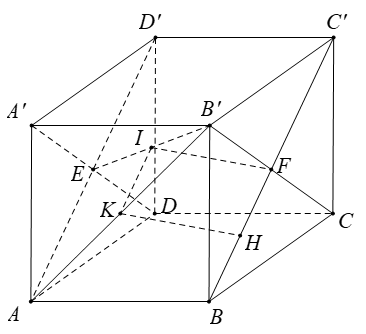
cho hình lập phương ABCD,A'B'C'D' biết AB=3cm a) cho biết độ dài các cạnh còn lại b) tính Sxq;Stp hình lập phương c) tính V hình lập phương

Những câu hỏi liên quan
Cho hình lập phương ABCD. A'B'C'D' cạnh a
a) Chứng minh BC' vuông góc với mặt phẳng (A'B'CD)
b) Xác định và tính độ dài đoạn vuông góc chung của AB' và B'C
Cho khối lập phương ABCD ABCD Người ta dùng 12 mặt phẳng phân biệt (trong đó, 4 mặt song song với (ABCD), 4 mặt song song với (AABB)và 4 mặt song song với (AADD)), chia khối lập phương nhỏ rời nhau và bằng nhau. Biết rằng tổng diện tích tất cả các khối lập phương nhỏ bằng 480. Tính độ dài a của khối lập phương ABCD ABCD A. a2 B.
a
2
3
.
C.
a
2
5
.
D.a4
Đọc tiếp
Cho khối lập phương ABCD A'B'C'D' Người ta dùng 12 mặt phẳng phân biệt (trong đó, 4 mặt song song với (ABCD), 4 mặt song song với (AA'B'B)và 4 mặt song song với (AA'D'D)), chia khối lập phương nhỏ rời nhau và bằng nhau. Biết rằng tổng diện tích tất cả các khối lập phương nhỏ bằng 480. Tính độ dài a của khối lập phương ABCD A'B'C'D'
A. a=2
B. a = 2 3 .
C. a = 2 5 .
D.a=4
Đáp án D
Diện tích toàn phần của hình lập phương cạnh a là S t p = 6 a 2 .
Khi dùng các mặt phẳng như đề bài cho để chia khối lập phương ABCD.A’B’C’D’ ta được 125 khối lập phương nhỏ bằng nhau.
Do đó diện tích toàn phần của 1 khối lập phương nhỏ là 480 125 = 96 25
Gọi cạnh hình lập phương ABCD.A’B’C’D’ bằng a thì độ dài cạnh hình lập phương nhỏ bằng a 5 .
Suy ra diện tích toàn phần của 1 hình lập phương nhỏ là: 6 a 5 2 = 96 25 ⇔ a = 4
Đúng 0
Bình luận (0)
Cho hình thang vuông ABCD có góc A = D = 90 độ, đường chéo BD vuông góc với cạnh BC và BD = BC a) Tính các góc của hình thang b) Biết AB = 3cm. Tính độ dài các cạnh BC và CD
a: \(\widehat{C}=45^0\)
\(\widehat{B}=135^0\)
Đúng 0
Bình luận (0)
Cho hình thang vuông ABCD có góc A= góc D =90°, đường chéo BD vuông góc với cạnh bên BC và BD=BC
a) Tính các góc của hình thang
b)Biết AB=3cm. Tính độ dài các cạnh BC và CD.
Xem chi tiết
Cho hình lập phương ABCD ABCD có cạnh bằng a. Tính theo a khoảng cách giữa hai đường thẳng AB và BC. A.
a
3
3
B.
a
2
3
C.
a
3
2
D.
a
2
2
Đọc tiếp
Cho hình lập phương ABCD A'B'C'D' có cạnh bằng a. Tính theo a khoảng cách giữa hai đường thẳng AB' và BC'.
A. a 3 3
B. a 2 3
C. a 3 2
D. a 2 2
Đáp án A.
Đặt B ' 0 ; 0 ; 0 , A ' a ; 0 ; 0 , C ' 0 ; a ; 0 , B 0 ; 0 ; a ⇒ A a ; 0 ; a
Ta có B ' A → = a ; 0 ; a , B C ' → = 0 ; a ; − a , B ' B → = 0 ; 0 ; a
⇒ B ' A → , B C ' → = − a 2 ; a 2 ; a 2 ; B ' A → , B C ' → . B B ' → = a 3
d B ' A , B C ' = B ' A → , B C ' → . B B ' → B ' A → , B C ' → = a 3 3 a 4 = a 3 a 2 3 = a 3 3
Đúng 0
Bình luận (0)
Cho hình lập phương ABCD. ABCD có cạnh bằng a. Gọi O và O lần lượt là tâm các hình vuông ABCD và ABCD. Gọi M, N lần lượt là trung điểm của các cạnh BC và CD. Tính thể tích khối tứ diện OOMN. A.
a
3
8
B. a3 C.
a
3
12
D.
a
3
24
Đọc tiếp
Cho hình lập phương ABCD. A'B'C'D' có cạnh bằng a. Gọi O và O' lần lượt là tâm các hình vuông ABCD và A'B'C'D'. Gọi M, N lần lượt là trung điểm của các cạnh B'C' và CD. Tính thể tích khối tứ diện OO'MN.
A. a 3 8
B. a3
C. a 3 12
D. a 3 24
Chọn D
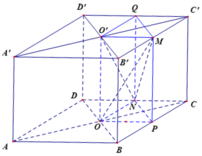
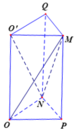
Gọi P, Q lần lượt là trung điểm của BC và C'D'.
Ta có S ∆ O P N = 1 4 S ∆ B C D = 1 8 S A B C D = a 2 8 ⇒ V O P N . O ' M Q = a 3 8
mà
V O O ' M N = V O P N . O ' M Q - V M . O P N - V N . O ' M Q = a 3 8 - 1 3 . a 3 8 - 1 3 . a 3 8 = a 3 24
Đúng 0
Bình luận (0)
hình thang vuông ABCD( AB// CD), A= 90 độ,có đường chéo BD vuông góc vs cạnh bên BC và bd=bc
a)tính các góc còn lại của hình thang
b)biết ab=3cm,tính cd và bc
1. Cho hình lập phương ABCD. A'B'C'D'. Xác định góc giữa 2 đg thẳng AC VÀ BC'. 2. Cho tứ diện đều ABCD góc giữa 2 vecto AB ,CD có số đo là? 3. Cho hình lập phương ABCD. A'B'C'D' có M,N lần lượt thuộc 2 cạnh AA' và DD' sao cho AN= NA' ; DD'=4DM . Tính cosa vs a= ( MN,B'D')
Cho hình lập phương ABCD. ABCD cạnh a. Tính khoảng cách từ B tới đường thẳng DB. A.
a
3
6
B.
a
6
3
C.
a
3
3
D.
a
6
6
Đọc tiếp
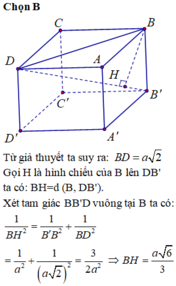
Cho hình lập phương ABCD. A'B'C'D' cạnh a. Tính khoảng cách từ B tới đường thẳng DB'.
A. a 3 6
B. a 6 3
C. a 3 3
D. a 6 6
Cho hình lập phương ABCD. ABCD có cạnh bằng a, gọi
α
là góc giữa đường thẳng AB và mặt phẳng (BBDD). Tính A.
3
4
B.
3
2
C.
3
5
D.
1
2
Đọc tiếp
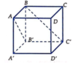
Cho hình lập phương ABCD. A'B'C'D' có cạnh bằng a, gọi α là góc giữa đường thẳng AB' và mặt phẳng (BB'D'D). Tính
A. 3 4
B. 3 2
C. 3 5
D. 1 2
Đáp án D
Gọi I là giao điểm của AC và BD
A I ⊥ B D A I ⊥ B B ' ⇒ A I ⊥ B B ' D ' D
=> B’I là hình chiếu vuông góc của AB’ lên (BB’D’D)
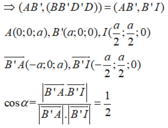
Đúng 0
Bình luận (0)