tìm x thoả mãn
3x-1+5.3x-1=162

Những câu hỏi liên quan
Tìm x
a) 5x+5x+2=650
b) 3x.1+5.3x.1=162
\(a,5^x+5^{x+2}=650\\ \Rightarrow a,5^x+5^x.25=650\\ \Rightarrow26.5^x=650\\ \Rightarrow5^x=25\\ \Rightarrow5^x=5^2\\ \Rightarrow x=2\)
\(b,3^{x.1}+5.3^{x.1}=162\\ \Rightarrow3^x+5.3^x=162\\ \Rightarrow6.3^x=162\\ \Rightarrow3^x=27\\ \Rightarrow3^x=3^3\\ \Rightarrow x=3\)
Đúng 2
Bình luận (0)
a: \(\Leftrightarrow5^x=25\)
hay x=2
Đúng 1
Bình luận (0)
a, <=> 5x + 5x .52 =650
<=> 5x +25.5x =650
<=> 26.5x =650
<=> 5x =25
<=> 5x = 52
<=> x=2
b, <=> 6. 3x =162
<=> 3x =27
<=> 3x =33
<=> x=3
Chúc bạn học tốt nha!
Đúng 1
Bình luận (0)
tìm x nguyên :9x+5 là tích của 2 số nguyên liên tiếp
tìm x,y nguyên thoả mãn :xy+3x-y=6
tìm x,y nguyên thoả mãn :x2−22=1x2−2y2=1
tìm x,y nguyên thoả mãn :xy+3x-y=6
1) Giả sử: \(9x+5=n\left(n+1\right)\left(n\in Z\right)\)
\(36x+20-4n^2+4n\)
\(\Rightarrow36x+21=4n^2+4n+1\)
\(\Rightarrow3\left(12x+7\right)=\left(2n+1\right)^2\)
\(\left(2n+1\right)^2\)là số chính phương nên sẽ chia hết cho 3 => (2n+1)2 chia hết cho 9
Lại có: 12x+7 ko chia hết cho 3 => 3(12x+7) ko chia hết cho 9
Chứng tỏ không tồn tại số nguyên x nào để 9x+5=n(n+1)
Đúng 0
Bình luận (0)
2) Ta có: xy + 3x - y = 6 =>x(y+3) - y = 6
=>x(y+3) - y - 3 = 3 =>x(y+3) - (y+3) = 3
=> (y+3)(x-1) =3
Vì x, y là các số nguyên nên y+3;x-1 là các số nguyên
Ta có bảng sau:
| y+3 | -3 | -1 | 1 | 3 |
| y | -6 | -4 | -2 | 0 |
| x-1 | -1 | -3 | 3 | 1 |
| x | 0 | -2 | 4 | 2 |
Đúng 0
Bình luận (0)
a, Tìm số thực thoả mãn I 3x - 1I = I 2x + 5I
b, Tìm số thực x,y,z thoả mãn (x-1)2 + I3y-1I + Iz+2I = 0
\(\left|3x-1\right|=\left|2x+5\right|\)
\(\Rightarrow\orbr{\begin{cases}3x-1=2x+5\\3x-1+2x+5=0\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}3x-2x=5+1\\5x+4=0\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=6\\x=-\frac{4}{5}\end{cases}}\)
Đúng 0
Bình luận (0)
Ta có: \(\hept{\begin{cases}\left(x-1\right)^2\ge0\\\left|3y-1\right|\ge0\\\left|z+2\right|\ge0\end{cases}}\Rightarrow\left(x-1\right)^2+\left|3y-1\right|+\left|z+2\right|\ge0\)
Dấu "="\(\Leftrightarrow\hept{\begin{cases}\left(x-1\right)^2=0\\\left|3y-1\right|=0\\\left|z+2\right|=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x-1=0\\3y-1=0\\x+2=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=1\\y=\frac{1}{3}\\z=-2\end{cases}}\)
Vậy x = 1, \(y=\frac{1}{3}\),z = -2
Đúng 0
Bình luận (0)
Tìm số nguyên x thoả mãn: 3x-|2x+1|=2
3x- I2x+1I=2
Có 2 trường hợp:
1) 3x-2x+1=2
x+1=2
Vậy x=1
3x-2x+1= -2
x+1 = -2
Vậy x= -3
Đúng 0
Bình luận (0)
Tìm x thoả mãn hệ phương trình
3
x
+
2
y
5
2
3
x
....
Đọc tiếp
Tìm x thoả mãn hệ phương trình 3 x + 2 y = 5 2 3 x . 2 y = 1
![]()
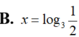
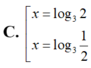
![]()
Tìm x , y,thuộc z thoả mãn : 3x (y+1)=y+5
Tìm giá trị của x thoả mãn 6x^2-(2x-3)(3x=2)-1=0
tìm x thoả mãn
(2x-1)(2x-5)<0
(3-2x)(x+2)>0
(3x+1)(5-2x)>0
mình đang rất cần
(2\(x\) - 1).(2\(x\) - 5) < 0
Lập bảng ta có:
| \(x\) | \(\dfrac{1}{2}\) \(\dfrac{5}{2}\) |
| 2\(x\) - 1 | - 0 + + |
| 2\(x\) - 5 | - - 0 + |
| (2\(x\) - 1).(2\(x\) - 5) | + 0 - 0 + |
Theo bảng trên ta có: \(\dfrac{1}{2}\) < \(x\) < \(\dfrac{5}{2}\)
Đúng 1
Bình luận (0)
(3 - 2\(x\)).(\(x\) + 2) > 0
Lập bảng ta có:
| \(x\) | -2 \(\dfrac{3}{2}\) |
| 3 - 2\(x\) | + + 0 - |
| \(x\) + 2 | - 0 + + |
| (3 -2\(x\)).(\(x\) +2) | - 0 + 0 - |
Theo bảng trên ta có: - 2 < \(x\) < \(\dfrac{3}{2}\)
Đúng 1
Bình luận (0)
(3\(x\) + 1).(5 - 2\(x\)) > 0
Lập bảng ta có:
| \(x\) | - \(\dfrac{1}{3}\) \(\dfrac{5}{2}\) |
| 3\(x\) + 1 | - 0 + + |
| 5 - 2\(x\) | + + 0 - |
| (3\(x\) + 1).(5 - 2\(x\)) | - 0 + 0 - |
Theo bảng trên ta có: - \(\dfrac{1}{3}\) < \(x\) < \(\dfrac{5}{2}\)
Đúng 1
Bình luận (0)
3x+1+5.3x+2=144
(x+1;x+2 là số mũ nhé bạn)
mà 3x+2 là riêng x thôi hay cả 3x ậy bạn
theo tớ là riêng x thôi. mà đề bài là dấu cộng mà.
Xem thêm câu trả lời
























