
mn giúp với mai em phải nộp rồi
Mọi người ai làm giúp em câu 4 với được không ạ, mai em phải nộp rồi, cảm ơn mn nhiều.
Ai làm giúp em câu 3 và 4 này với được không ạ, mai em phải nộp rồi, cảm ơn mn nhiều.
Ai làm giúp mình câu 2 này với được không ạ, mai em phải nộp rồi, cảm ơn mn nhiều. 
Ai làm giúp mình câu 6 này với được không ạ, mai em phải nộp rồi, cảm ơn mn nhiều.
\(a,m=3\Leftrightarrow y=2x+2\\ A\left(a;-4\right)\in\left(d\right)\Leftrightarrow2a+2=-4\Leftrightarrow a=-3\)
\(b,\) PT giao Ox của (d) là \(2x+m-1=0\Leftrightarrow x=\dfrac{1-m}{2}\Leftrightarrow M\left(\dfrac{1-m}{2};0\right)\Leftrightarrow OM=\dfrac{\left|1-m\right|}{2}\)
PT giao Oy của (d) là \(x=0\Leftrightarrow y=m-1\Leftrightarrow N\left(0;m-1\right)\Leftrightarrow ON=\left|m-1\right|\)
Để \(S_{OMN}=1\Leftrightarrow\dfrac{1}{2}OM\cdot ON=1\Leftrightarrow OM\cdot ON=2\)
\(\Leftrightarrow\dfrac{\left|\left(1-m\right)\left(m-1\right)\right|}{2}=2\\ \Leftrightarrow\left|-\left(m-1\right)^2\right|=2\\ \Leftrightarrow\left(m-1\right)^2=2\\ \Leftrightarrow\left[{}\begin{matrix}m=1+\sqrt{2}\\m=1-\sqrt{2}\end{matrix}\right.\)
Mọi người làm giúp em câu 3 và 4 này với được không ạ, mai em phải nộp rồi, cảm ơn mn nhiều.
Bài 3:
Gọi K là giao của AH và BC thì AK là đường cao thứ 3 (H là trực tâm)
Vì \(\widehat{BDC}=\widehat{BEC}=90^0\) nên BEDC nội tiếp
Lại có \(BI=IC=ID=IE=\dfrac{1}{2}BC\) (trung tuyến ứng cạnh huyền) nên I là tâm đg tròn ngoại tiếp BDEC
Gọi G là trung điểm AH thì \(AG=GD=DE=\dfrac{1}{2}AH\) (trung tuyến ứng ch)
Do đó G là tâm () ngoại tiếp tg ADE
Vì \(GA=GD\Rightarrow\widehat{DAG}=\widehat{GDA}\)
Vì \(ID=IB\Rightarrow\widehat{ABI}=\widehat{IDB}\)
Do đó \(\widehat{IDB}+\widehat{GDA}=\widehat{DAG}+\widehat{ABI}=90^0\left(\Delta AKB\perp K\right)\)
Do đó \(\widehat{IDG}=180^0-\left(\widehat{IDB}+\widehat{GDA}\right)=90^0\)
Vậy \(ID\perp IG\) hay ...
Ai làm giúp mình câu 8 và 9 này với được không ạ, mai em phải nộp rồi, cảm ơn mn nhiều.

8.
Gọi \(A\left(x_0;y_0\right)\) là điểm cố định mà đt luôn đi qua với mọi m
\(\Leftrightarrow mx_0+2y_0-3my_0+m-1=0\\ \Leftrightarrow m\left(x_0-3y_0+1\right)+\left(2y_0-1\right)=0\\ \Leftrightarrow\left\{{}\begin{matrix}x_0-3y_0+1=0\\2y_0-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=\dfrac{1}{2}\\y_0=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow A\left(\dfrac{1}{2};\dfrac{1}{2}\right)\)
Vậy đt luôn đi qua \(A\left(\dfrac{1}{2};\dfrac{1}{2}\right)\) với mọi m
9.
PT giao Ox là \(y=0\Leftrightarrow mx+m-1=0\Leftrightarrow x=\dfrac{1-m}{m}\Leftrightarrow A\left(\dfrac{1-m}{m};0\right)\Leftrightarrow OA=\left|\dfrac{1-m}{m}\right|\)
PT giao Oy là \(x=0\Leftrightarrow\left(2-3m\right)y+m-1=0\Leftrightarrow y=\dfrac{1-m}{2-3m}\Leftrightarrow B\left(0;\dfrac{1-m}{2-3m}\right)\Leftrightarrow OB=\left|\dfrac{1-m}{2-3m}\right|\)
Để \(\Delta OAB\) cân thì \(OA=OB\Leftrightarrow\left|\dfrac{1-m}{m}\right|=\left|\dfrac{1-m}{2-3m}\right|\)
\(\Leftrightarrow\left|m\right|=\left|2-3m\right|\Leftrightarrow\left[{}\begin{matrix}m=2-3m\\m=3m-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{1}{2}\\m=1\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}m=\dfrac{1}{2}\\m=1\end{matrix}\right.\) thỏa mãn đề
Mn giúp em câu này với, tối mai em nộp rồi
Mn giúp em câu này với ạ
Tối mai em nộp rồi
Mn làm giúp mình bài 3, 4 với ạ. Mai mình phải nộp rồi
Bài 3:
PTHH: \(2R+O_2\xrightarrow[]{t^O}2RO\)
Theo PTHH: \(n_R=n_{RO}\) \(\Rightarrow\dfrac{3,6}{M_R}=\dfrac{6}{M_R+16}\)
\(\Rightarrow M_R=24\) (Magie)
Bài 2:
PTHH: \(2Al+6HCl\rightarrow2AlCl_3+3H_2\uparrow\)
Ta có: \(n_{Al}=\dfrac{8,1}{27}=0,3\left(mol\right)\)
\(\Rightarrow\left\{{}\begin{matrix}n_{HCl}=0,9\left(mol\right)\\n_{AlCl_3}=0,3\left(mol\right)\\n_{H_2}=0,45\left(mol\right)\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}V_{H_2}=0,45\cdot22,4=10,08\left(l\right)\\m_{AlCl_3}=0,3\cdot133,5=40,05\left(g\right)\\m_{ddHCl}=\dfrac{0,9\cdot36,5}{7,3\%}=450\left(g\right)\\m_{H_2}=0,45\cdot2=0,9\left(g\right)\end{matrix}\right.\)
Mặt khác: \(m_{dd\left(saup/ứ\right)}=m_{Al}+m_{ddHCl}-m_{H_2}=457,2\left(g\right)\)
\(\Rightarrow C\%_{AlCl_3}=\dfrac{40,05}{457,2}\cdot100\%\approx8,76\%\)
Ai làm giúp mình câu 3 này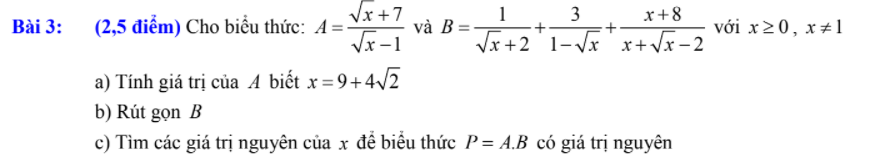 được không ạ, mai em phải nộp rồi, cảm ơn mn nhiều.
được không ạ, mai em phải nộp rồi, cảm ơn mn nhiều.
a: Thay \(x=9+4\sqrt{2}\) vào A, ta được:
\(A=\dfrac{2\sqrt{2}+1+7}{2\sqrt{2}+1-1}=\dfrac{8+2\sqrt{2}}{2\sqrt{2}}=2\sqrt{2}+1\)