Tìm các số tự nhiên a và b thỏa mãn a+b=120 và (a,b)=15

Những câu hỏi liên quan
Tìm các số tự nhiên a, b thỏa mãn a+b=120 và (a, b)=15
Tìm các số tự nhiên a , b thõa mãn a+b=120 và [a,b]=15
tìm các số tự nhiên a và b (a;b) thỏa mãn UWCLN (a;b)+12 và BCNN (a;b) =240
Ta có :
a . b = ƯCLN ( a , b ) . BCNN ( a , b )
=> a . b = 12 . 240 =
=> a . b = 2880
Vì ƯCLN ( a , b ) = 12
=> a = 12m
b = 12 . n ( m , n ) = 1
=> a . b = 12m . 12n = 144 . mn = 2880
=> mn = 2880 : 144
=> mn = 20
Ta thấy 20 = 1 . 20 = 2 . 10 = 4 . 5
Vì ( m , n ) = 1
=> ( m , n ) = ( 1 ; 20 ) , ( 20 ; 1 ) , ( 4 ; 5 ) , ( 5 ; 4 )
=> ( a , b ) = ( 12 ; 240 ) , ( 240 ; 12 ) , ( 48 , 60 ) , ( 60 ; 48 )
Vậy ab = ( 12 ; 240 )
= ( 240 ; 12 )
= ( 48 ; 60 )
= ( 60 ; 48 )
tìm hai số tự nhiên a,b thỏa mãn
2a-3b=100 và 15.BCNN(a,b)+8.ƯCLN(a,b)=1990
Tìm các cặp số tự nhiên a,b sao thỏa mãn a+b=92 và (a,b)+[a,b]=484
Đặt (a;b) = d thì a = dm ; b = dn (m,n \(\in\) N*)
Ta có : a + b = dm + dn = d(m + n) = 92 (1)
và [a;b] = [dm;dn] = dmn
=> (a;b) + [a;b] = d + dmn = d(1 + mn) = 484 (2)
Từ (1) và (2) => ......
Đúng 0
Bình luận (0)
tìm các số tự nhiên a b c thỏa mãn 2 điều kiện 16<a<b và 20>c>b
` 16<a<b`
`20>c>b`
`=>16<a<b<b<20/
`=> a= 17`
`b = 18`
`c = 19`
Đúng 1
Bình luận (0)
Tìm số tự nhiên để 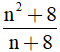 là số tự nhiên.
là số tự nhiên.
Cho các số a, b thỏa mãn a + b = 2 và a.b = - 2. Tính a7 + b7.
a: Để A là số tự nhiên thì \(n+8\in\left\{8;9;12;18;24;36;72\right\}\)
hay \(n\in\left\{0;1;3;10;18;28;64\right\}\)
Đúng 0
Bình luận (0)
Tìm các số tự nhiên a và b thỏa mãn (5a + 7b) / 6a +5b = 29/28 và (a; b) = 1
a) Tìm số tự nhiên n biết (4n+2) ⋮ (n+1)
b) Tìm các số nguyên a và b thỏa mãn: (a+2).(b-1)=9
Cíuuu tuiiii
a: =>4n+4-2 chia hết cho n+1
=>\(n+1\in\left\{1;-1;2;-2\right\}\)
mà n là số tự nhiên
nên \(n\in\left\{0;1\right\}\)
b: \(\Leftrightarrow\left(a+2;b-1\right)\in\left\{\left(1;9\right);\left(9;1\right);\left(-1;-9\right);\left(-9;-1\right);\left(3;3\right);\left(-3;-3\right)\right\}\)
=>\(\left(a,b\right)\in\left\{\left(-1;10\right);\left(7;2\right);\left(-3;-8\right);\left(-11;0\right);\left(1;4\right);\left(-5;-2\right)\right\}\)
Đúng 0
Bình luận (0)






















