a) Đây là phép chia ết với đa thức thương  x 2  + 2x + 1.

Có thể kiểm tra lại kết quả bằng cách thực hiện nhân hai đa thức (x – 3)( x 2  + 2x +1)

b) Đa thức thương  x 2  – 5.

b: \(=\dfrac{2x^4-2x^3-2x^2-3x^3+3x^2+3x+x^2-x-1}{x^2-x-1}\)

\(=2x^2-3x+1\)

Bài 1: 

a: \(=\dfrac{2x^4-8x^3+2x^2+2x^3-8x^2+2x+18x^2-72x+18+56x-15}{x^2-4x+1}\)

\(=2x^2+2x+18+\dfrac{56x-15}{x^2-4x+1}\)

Để \(x^4-x^3+6x^2-x+n⋮x^2-x+5\) thì

\(n-5=0\Rightarrow n=5\)

Vậy để \(x^4-x^3+6x^2-x+n⋮x^2-x+5\) thì \(n=5\)

1) \(\left(x^3-8\right):\left(x-2\right)=\left[\left(x-2\right)\left(x^2+2x+4\right)\right]:\left(x-2\right)=x^2+2x+4\)

2) \(\left(x^3-1\right):\left(x^2+x+1\right)=\left[\left(x-1\right)\left(x^2+x+1\right)\right]:\left(x^2+x+1\right)=x-1\)

3) \(\left(x^3+3x^2+3x+1\right):\left(x^2+2x+1\right)=\left(x+1\right)^3:\left(x+1\right)^2=x+1\)

4) \(\left(25x^2-4y^2\right):\left(5x-2y\right)=\left[\left(5x-2y\right)\left(5x+2y\right)\right]:\left(5x-2y\right)=5x+2y\)

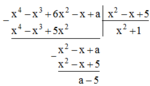
Để có phép chia hết thì số dư phải bằng 0.

Ta có: a – 5 = 0 hay a = 5.

b: \(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)

\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)

\(\Leftrightarrow n\in\left\{0;-1;1\right\}\)

(125x3 + 1) : (5x + 1)

= [(5x)3 + 1] : (5x + 1)

= (5x + 1)[(5x)2 – 5x + 1]] : (5x + 1)

= (5x)2 – 5x + 1

= 25x2 – 5x + 1

Bài 3:

Ta có: \(2n^2+n-7⋮n-2\)

\(\Leftrightarrow2n^2-4n+5n-10+3⋮n-2\)

\(\Leftrightarrow n-2\in\left\{1;-1;3;-3\right\}\)

hay \(n\in\left\{3;1;5;-1\right\}\)

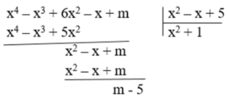
A(x) chia cho B(x) có số dư bằng 2. Vậy m – 5 = 2 ⇒ m = 7.