cho hình vuông ABCD trên cạnh BC lấy M trên tia đối của DC lấy N sao cho BM = DN khi đó số đo góc AMN là

Những câu hỏi liên quan
Bài 1. Cho hình vuông ABCD có cạnh bằng a. Trên cạnh BC lấy điểm M, trên tia đối của tia DC lấy điểm N sao cho BM = DN. a) Chứng minh tam giác AMN là tam giác vuông cân. b) Gọi E là trung điểm của MN. Tia AE cắt CD tại F. Chứng minh tam giác FAN = tam giác FAM.
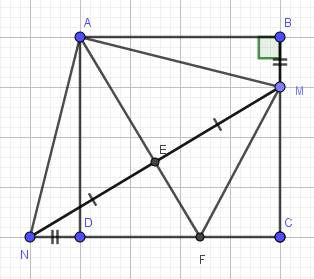
a) Do ABCD là hình vuông (gt)
\(\Rightarrow AB=AD\)
\(\widehat{ABM}=\widehat{ADN}=90^0\)
Xét hai tam giác vuông: \(\Delta ABM\) và \(\Delta ADN\) có:
\(AB=AD\left(cmt\right)\)
\(BM=DN\left(gt\right)\)
\(\Rightarrow\Delta ABM=\Delta ADN\) (hai cạnh góc vuông)
\(\Rightarrow AM=AN\) (hai cạnh tương ứng)
\(\widehat{BAM}=\widehat{DAN}\) (hai góc tương ứng)
Ta có:
\(\widehat{BAM}+\widehat{DAM}=90^0\)
\(\Rightarrow\widehat{DAN}+\widehat{DAM}=90^0\)
\(\Rightarrow\widehat{MAN}=90^0\)
\(\Delta AMN\) có:
\(AM=AN\left(cmt\right)\)
\(\Rightarrow\Delta AMN\) cân tại A
Mà \(\widehat{MAN}=90^0\left(cmt\right)\)
\(\Rightarrow\Delta AMN\) vuông cân tại A
b) Do \(\Delta AMN\) cân tại A
E là trung điểm của MN
\(\Rightarrow AE\) là đường trung tuyến, cũng là đường cao của \(\Delta AMN\)
\(\Rightarrow AE\perp MN\)
\(\Rightarrow EF\perp MN\)
Xét hai tam giác vuông: \(\Delta FEM\) và \(\Delta FEN\) có:
\(EM=EN\left(gt\right)\)
\(EF\) là cạnh chung
\(\Rightarrow\Delta FEM=\Delta FEN\) (hai cạnh góc vuông)
\(\Rightarrow FM=FN\) (hai cạnh tương ứng)
Xét \(\Delta FAN\) và \(\Delta FAM\) có:
\(FA\) là cạnh chung
\(FN=FM\left(cmt\right)\)
\(AN=AM\left(cmt\right)\)
\(\Rightarrow\Delta FAN=\Delta FAM\left(c-c-c\right)\)
Đúng 3
Bình luận (0)
Cho hình vuông ABCD. Trên cạnh BC lấy điểm M, trên tia đối của tia DC lấy điểm N sao cho BM=DN.
a, CMR tam giác ABM=ADN
b,CMR tam giác AMN vuông cân
c,Tia phân giác của góc MAN cắt CD tại P. CMR MP=BM+DP
d,Gọi AP cắt MN tại I. CMR MP=BM+DP
a: Xét ΔABM vuông tại B và ΔADN vuông tại D có
AB=AD
BM=DN
Do đó: ΔABM=ΔADN
b: ΔABM=ΔADN
=>AM=AN và \(\widehat{MAB}=\widehat{NAD}\)
\(\widehat{MAB}+\widehat{DAM}=\widehat{BAD}=90^0\)
mà \(\widehat{MAB}=\widehat{NAD}\)
nên \(\widehat{DAM}+\widehat{DAN}=90^0\)
=>\(\widehat{MAN}=90^0\)
Xét ΔAMN có AM=AN và \(\widehat{MAN}=90^0\)
nênΔAMN vuông cân tại A
d: ΔAMN cân tại A
mà AI là đường phân giác
nên I là trung điểm của MN và AI\(\perp\)MN tại I
=>AP\(\perp\)MN tại I
Xét ΔPNM có
PI là đường cao
PI là đường trung tuyến
Do đó: ΔPNM cân tại P
=>PN=PM
=>PM=PD+DN=PD+BM
Đúng 0
Bình luận (0)
Cho hình vuông ABCD cố định, M là 1 điểm lấy trên cạnh BC (M B). Tia AM cắt DC tại P. Trên tia đối của tia DC lấy điểm N sao cho DN BM. a. Chứng minh: AND ABM và MAN là vuông cân.b. Chứng minh: ABM và PDA đồng dạng và BC2 BM . DP. c. Qua A vẽ đường thẳng vuông góc với MN tại H và cắt CD tại Q, MN cắt AD ở I. Chứng minh: AH . AQ AI . AD và DÂQ HMQ.d. Chứng minh: NDH và NIQ đồng dạng
Đọc tiếp
Cho hình vuông ABCD cố định, M là 1 điểm lấy trên cạnh BC (M B). Tia AM cắt DC tại P. Trên tia đối của tia DC lấy điểm N sao cho DN = BM.
a. Chứng minh: AND = ABM và MAN là vuông cân.
b. Chứng minh: ABM và PDA đồng dạng và BC2 = BM . DP.
c. Qua A vẽ đường thẳng vuông góc với MN tại H và cắt CD tại Q, MN cắt AD ở I. Chứng minh: AH . AQ = AI . AD và DÂQ = HMQ.
d. Chứng minh: NDH và NIQ đồng dạng
Cho hình vuông ABCD cạnh bằng a. Trên hai cạnh BC, CD lấy lần lượt hai điểm M, N sao cho M A N ^ = 45 0 . Trên tia đối của của tia DC lấy điểm K sao cho DK = BM. Hãy tính: Tính số đo K A N ^ = ?
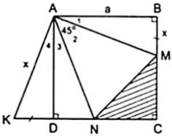
Áp dụng đĩnh nghĩa và giả thiết của hình vuông ABCD, ta được
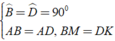
⇒ Δ ABM = Δ ADK ( c - g - c )
Áp dụng kết quả của hai tam giác bằng nhau và giả thiết, ta có:
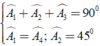
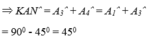
Đúng 0
Bình luận (0)
Cho hình vuông ABCD cạnh bằng a. Trên hai cạnh BC, CD lấy lần lượt hai điểm M, N sao cho M A N ^ = 45 0 . Trên tia đối của của tia DC lấy điểm K sao cho DK = BM. Hãy tính: Tính số đo K A N ^ = ?
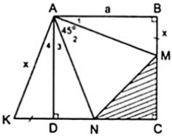
a) Áp dụng đĩnh nghĩa và giả thiết của hình vuông ABCD, ta được
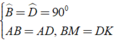
⇒ Δ ABM = Δ ADK ( c - g - c )
Áp dụng kết quả của hai tam giác bằng nhau và giả thiết, ta có:
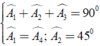
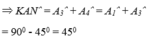
Đúng 0
Bình luận (0)
Cho hình vuông ABCD cạnh bằng a. Trên hai cạnh BC, CD lấy lần lượt hai điểm M, N sao cho M A N ^ = 45 0 . Trên tia đối của của tia DC lấy điểm K sao cho DK = BM. Hãy tính: Tính số đo K A N ^ = ?
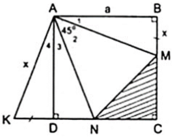
a) Áp dụng đĩnh nghĩa và giả thiết của hình vuông ABCD, ta được
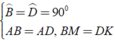
⇒ Δ ABM = Δ ADK ( c - g - c )
Áp dụng kết quả của hai tam giác bằng nhau và giả thiết, ta có:
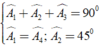
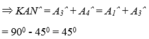
Đúng 0
Bình luận (0)
Cho hình vuông ABCD cạnh bằng a. Trên hai cạnh BC, CD lấy lần lượt hai điểm M, N sao cho M A N ^ = 45 0 . Trên tia đối của của tia DC lấy điểm K sao cho DK = BM. Hãy tính : Tính số đo K A N ^ = ?
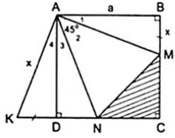
Áp dụng đĩnh nghĩa và giả thiết của hình vuông ABCD, ta được
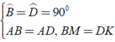 ⇒ Δ ABM = Δ ADK ( c - g - c )
⇒ Δ ABM = Δ ADK ( c - g - c )
Áp dụng kết quả của hai tam giác bằng nhau và giả thiết, ta có:
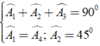
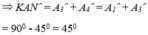
Đúng 0
Bình luận (0)
cho hình vuông ABCD có cạnh bằng a. Trên BC là M, trên tia đối của tia DC lấy N sao cho BM=DN. Vẽ AH vuông góc với NM (H thuộc NM), AH cắt DC tại E. Gọi G là giao điểm của MN với AD. a. Chứng minh tam giác NAM vuông cân và D,H,B thẳng hàng.
Cho hình vuông ABCD cạnh a. Trên các cạnh BC và CD lấy 2 điểm M, N sao cho góc MAN=45 độ. Trên tia đối của tia DC lấy điểm E sao cho DE=BM
a)cm AE=AM rồi từ đó suy ra AN vuông góc EM
b) tìm vị trí M thuộc BC và N thuộc CD sao cho diện tích tam giác AMN lớn nhất












