_Tìm x (x thuộc N*) sao cho Q = x3 + x2 + 2025 là một số chính phương nhỏ hơn 10000

Những câu hỏi liên quan
Tìm tất cả các số nguyên dương x sao cho x^3 + x^2 + 2025 là một số chính phương nhỏ hơn 10000
Giả sử \(x^3+x^2+2025\) là số chính phương nhỏ hơn 10000. Ta có phương trình:
\(x^3+x^2+2025 =k^2(k \in N,k^2<10000 \Leftrightarrow
k<100)\)
\(\Leftrightarrow
\)\(2025=k^2-x^2(x+1)\)
\(\Leftrightarrow
\)\(2025=(k-x\sqrt{x+1})(k+x\sqrt{x+1})\)
Mà \(k-x\sqrt{x+1} < k+x\sqrt{x+1}< 100\)(Vì \(k < 100\))
\(\Rightarrow \)\(\left[\begin{array}{}
\begin{cases}
k+x\sqrt{x+1}=81\\
k-x\sqrt{x+1}=25
\end{cases}\\
\begin{cases}
k+x\sqrt{x+1}=75\\
k-x\sqrt{x+1}=27
\end{cases}\\
\end{array} \right.\)
\(\Leftrightarrow\)\(\left[\begin{array}{}
\begin{cases}
2k=106\\
k-x\sqrt{x+1}=25
\end{cases}\\
\begin{cases}
2k=102\\
k-x\sqrt{x+1}=27
\end{cases}\\
\end{array} \right.\)
\(\Leftrightarrow\)\(\left[\begin{array}{}
\begin{cases}
k=53\\
53-x\sqrt{x+1}=25
\end{cases}\\
\begin{cases}
k=51\\
51-x\sqrt{x+1}=27
\end{cases}\\
\end{array} \right.\)
\(\Leftrightarrow\)\(\left[\begin{array}{}
\begin{cases}
k=53\\
x\sqrt{x+1}=28
\end{cases}\\
\begin{cases}
k=51\\
x\sqrt{x+1}=24
\end{cases}\\
\end{array} \right.\)
\(\Leftrightarrow\)\(\left[\begin{array}{}
\begin{cases}
k=53\\
x^3+x^2-784=0
\end{cases}\\
\begin{cases}
k=51\\
x^3+x^2-576=0
\end{cases}\\
\end{array} \right.\)
\(\Leftrightarrow\)\(\left[\begin{array}{}
\begin{cases}
k=53\\
x^3+x^2-784=0(PTVN)
\end{cases}\\
\begin{cases}
k=51\\
x^3-8x^2+9x^2-72x+72x-576=0
\end{cases}\\
\end{array} \right.\)
\(\Leftrightarrow\)\(\begin{cases}
k=51\\
(x-8)(x^2+9x+72)=0
\end{cases}\)
\(\Leftrightarrow\)\(\begin{cases}
k=51(t/m)\\
\left[\begin{array}{}
x=8(t/m)\\
(x+\frac{9}{2})^2+\frac{207}{4}=0(PTVN)
\end{array} \right.
\end{cases}\)
Vậy chỉ có giá trị \(x=8\) thỏa mãn yêu cầu bài toán.
P/s: Cái c/m vô nghiệm kia mình không biết làm. Chỉ biết bấm máy tính không ra nghiệm nguyên
Đúng 1
Bình luận (0)
_Tìm các số tự nhiên n sao cho: n2 + 16n + 2011 là 1 số chính phương
Đặt \(n^2+16n+2011=k^2\left(k\in N\right)\)
\(< =>\left(n^2+16n+64\right)+1947=k^2\)
\(< =>\left(n+8\right)^2+1947=k^2< =>k^2-\left(n+8\right)^2=1947\)
\(< =>\left(k-n-8\right)\left(k+n+8\right)=1947\)
Có \(k-n-8< k+n+8\)
\(=>\left(k-n-8\right)\left(k+n+8\right)=1.1947=3.649=11.177\)
bn tự giải tiếp nhé,đến đây dễ rồi
Đúng 0
Bình luận (0)
_bạn còn thiếu 1 trường hợp là 59 .33 nhé # CTV Hoàng Phúc
Đúng 0
Bình luận (0)
uk , tks , bn tự bổ sung ,mk k có máy tính nên k chắc chắn
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho phương trình (x-1)(x-3)(x-4)(x-12)=ax^2 (a là tham số). giả sử a nhận các giá trị sao cho phương trình có 4 nghiệm x1,x2,x3,x4 đều khác 0. CMR: S =\(\frac{1}{x1}+\frac{1}{x2}+\frac{1}{x3}+\frac{1}{x4}\) không phụ thuộc vào a.
giúp mình với =)
1,tìm các số nguyên dương x,y,z thoả mãn 3x2+6y2+z2+3y2z2-18x=6
2,tìm x là số tự nhiên sao cho Q=x3+x2+2025 là một số chính phương
Tìm 11 số tự nhiên liên tiếp có tổng các bình phương của chúng là một số chính phương nhỏ hơn 10000
Một vật thực hiện đồng thời ba dao động điều hòa cùng phương cùng tần số có li độ là
x
1
,
x
2
,
x
3
. Hình vẽ là đồ thị phụ thuộc thời gian của
x
12
x
1
+
x
2
(đường 1),
x
23
x
3
+
x
2
(đường 2),...
Đọc tiếp
Một vật thực hiện đồng thời ba dao động điều hòa cùng phương cùng tần số có li độ là x 1 , x 2 , x 3 . Hình vẽ là đồ thị phụ thuộc thời gian của x 12 = x 1 + x 2 (đường 1), x 23 = x 3 + x 2 (đường 2), x 31 = x 3 + x 1 (đường 3). Khi x = x 1 + x 2 + x 3 x2 đạt giá trị cực tiểu thì dao động x3 có li độ là
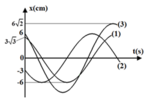
A. 0 cm và đang đi theo chiều dương
B. -3 cm và đang đi theo chiều âm
C. -3 cm và đang đi theo chiều dương
D. 3 2 cm và đang đi theo chiều âm
Đáp án C
Dựa vào đồ thị dễ dàng tìm được
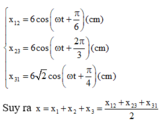
Dùng công cụ số phức của máy tính để bấm tổng hợp dao động, ta có
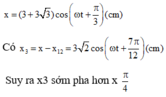
Khi x đạt giá trị cực tiểu (biên âm) thì
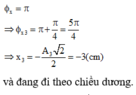
Đúng 0
Bình luận (0)
Cho số nguyên n>5 thỏa mãn, tồn tại các số nguyên dương x1,x2,x3,...,xn có tổng bằng 130 sao cho tổng của 5 số bất kì nhỏ hơn 26. hỏi n nhỏ nhất là bao nhiêu.
Cho số nguyên n>5 thỏa mãn, tồn tại các số nguyên dương x1,x2,x3,...,xn có tổng bằng 130 sao cho tổng của 5 số bất kì nhỏ hơn 26. hỏi n nhỏ nhất là bao nhiêu.
Tìm x thuộc n sao cho
x^2+2x+200 là số chính phương
x(x-1)(x-7)(x-8) la số chính phương
240m2
60m
180m
còn lời giải tự làm nhé!!!!!!!!!!!!!!!!!!!!
Đúng 0
Bình luận (0)














