Chứng minh rằng tam giác cân hai đường chí tuyền và 2 đường phân giác xuất phát từ đáy thì bằng nhau..Kèm hình vẽ nha

Những câu hỏi liên quan
bài 1: chứng minh 1 tam có 2 đường trung tuyến bằng nhau thì tam giác đó cân
bài 2: chứng minh trong tam giác cân 2 đường cao ứng với 2 cạnh bên và ngược lại có 2 đường cao bằng nhau là tam giác cân
bài 3:chứng minh 2 đường phân giác xuất phát từ 2 đỉnh ở đấy của tam giác cân thì bằng nhau và ngược lại 1 tam giác có 2 đg phân giác bằng nhau thì là tam giác ân
chứng minh rằng trong tam giác cân. độ dài các đường trung tuyến, đường cao, phân giác xuát phát từ hai đỉnh thuộc đáy thì bằng nhau?
mn giúp mk với nha cảm ơn rất nhìu
dễ ẹc!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
ko giúp!tự động não!
OK.!!!!!!!!
Chứng minh rằng một tam giác có hai đường đường cao(xuất phát từ các đỉng của hai góc nhọn) bằng nhau thì tam giác đó là tam giác cân. Từ đó suy ra một tam giác có ba đường cao bằng nhau thì tam giác đó là tam giác đều.
Xét hai tam giác vuông EBC và FCB có:
BC (cạnh huyền chung)
BE = CF
Vậy ∆EBC = ∆FCB (cạnh huyền cạnh góc vuông)
=> Góc FBC = góc ECB
hay ∆ABC cân tại A
Đúng 0
Bình luận (0)
Chứng minh rằng một tam giác có hai đường cao (xuất phát từ các đỉnh của hai góc nhọn) bằng nhau thì tam giác đó là tam giác cân. Từ đó suy ra một tam giác có ba đường cao bằng nhau thì tam giác đó là tam giác đều.
Hướng dẫn:
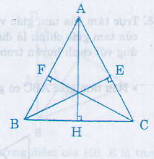
Xét hai tam giác vuông EBC và FCB có:
BC (cạnh huyền chung)
BE = CF (giả thiết)
Vậy ∆EBC = ∆FCB (cạnh huyền cạnh góc vuông)
=> \(\widehat{FBC}=\widehat{ECB}\)
hay ∆ABC cân tại A
+ Nếu tam giác có ba đường cao bằng nhau, tương tự như chứng minh trên, ta chứng minh được ba góc của chúng bằng nhau, suy ra đó là tam giác đều.
Đúng 1
Bình luận (1)

Xét hai tam giác vuông EBC và FCB có:
BC (cạnh huyền chung)
BE = CF
Vậy ∆EBC = ∆FCB (cạnh huyền cạnh góc vuông)
=> ˆFBC=ˆECBFBC^=ECB^
hay ∆ABC cân tại A
+ Nếu tam giác có ba đường cao bằng nhau, tương tự như chứng minh trên, ta chứng minh được đó là tam giác đều.
Đúng 0
Bình luận (0)
Chứng minh rằng một tam giác có hai đường cao (xuất phát từ các đỉnh của hai góc nhọn) bằng nhau thì tam giác đó là tam giác cân. Từ đó suy ra một tam giác có ba đường cao bằng nhau thì tam giác đó là tam giác đều.

Xét hai tam giác vuông EBC và FCB có:
BC (cạnh huyền chung)
BE = CF
Vậy ∆EBC = ∆FCB (cạnh huyền cạnh góc vuông)
=>
hay ∆ABC cân tại A
+ Nếu tam giác có ba đường cao bằng nhau, tương tự như chứng minh trên, ta chứng minh được đó là tam giác đều.
Đúng 0
Bình luận (0)
Chứng minh rằng một tam giác có hai đường cao (xuất phát từ các đỉnh của hai góc nhọn) bằng nhau thì tam giác đó là tam giác cân. Từ đó suy ra một tam giác có ba đường cao bằng nhau thì tam giác đó là tam giác đều.
mạng mạng
Vẽ BH⊥ACvà CK⊥AB
Xét hai tam giác vuông KBC và HCB có:
Cạnh BC chung
BH=CK(gt)
⇒ΔKBC=ΔHCB
⇒KBCˆ=HCBˆ
Xét tam giác ABC, có:
KBCˆ=HCBˆ hay ABCˆ=ACBˆ
Vậy tam giác ABC cân tại A (đpcm)
Ba đường cao bằng nhau
Từ a) ta có:
Nếu BH = CK thì ΔABC cân tại A => AB = AC (1)
Nếu AI = BH thì ΔABC cân tại C => CA = CB (2)
Từ (1) và (2) ta có: AB = BC = AC
Vậy ΔABC là tam giác đều.
Đúng 0
Bình luận (0)

Xét hai tam giác vuông EBC và FCB có:
BC (cạnh huyền chung)
BE = CF
Vậy ∆EBC = ∆FCB (cạnh huyền cạnh góc vuông)
\(\Rightarrow\widehat{FBC}=\widehat{ECB}\)
hay ∆ABC cân tại A
+ Nếu tam giác có ba đường cao bằng nhau, tương tự như chứng minh trên, ta chứng
minh được đó là tam giác đều.
Đúng 0
Bình luận (0)
chứng minh rằng trong một tam giác cân, đường cao xuất phát từ đỉnh đối diện với đáy đồng thời là đường phân giác cùng xuất phát từ đỉnh này
Chứng minh rằng 1 tam giác có 2 đường cao (xuất phát từ các đỉnh của 2 góc nhọn) bằng nhau thì tam giác đó là tam giác cân. Từ đó suy ra 1 tam giác có 3 đường cao bằng nhau là tam giác đều
Chứng minh phần " tam giác có 3 đường cao bằng nhau " giúp mình nha. Phần " tam giác có 2 đường cao bằng nhau " mình tự làm được

Xét hai tam giác vuông EBC và FCB có:
BC (cạnh huyền chung)
BE = CF
Vậy ∆EBC = ∆FCB (cạnh huyền cạnh góc vuông)
=>
hay ∆ABC cân tại A
+ Nếu tam giác có ba đường cao bằng nhau, tương tự như chứng minh trên, ta chứng minh được đó là tam giác đều.
Đúng 0
Bình luận (0)
tam giác abc có 2 đường phân giác xuất phát từ A,B bằng nhau chứng minh tam giác abc cân tại c



















