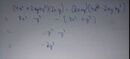a,sửa đề :  \(\left(\frac{1}{x^2+4x+4}-\frac{1}{x^2-4x+4}\right):\left(\frac{1}{x+2}+\frac{1}{x^2-4}\right)\)

\(=\left(\frac{1}{\left(x+2\right)^2}-\frac{1}{\left(x-2\right)^2}\right):\left(\frac{x-2+1}{\left(x+2\right)\left(x-2\right)}\right)\)

\(=\left(\frac{x^2-4x+4-x^2-4x-4}{\left(x+2\right)^2\left(x-2\right)^2}\right):\left(\frac{x-1}{\left(x+2\right)\left(x-2\right)}\right)\)

\(=\frac{-8x\left(x+2\right)\left(x-2\right)}{\left(x+2\right)^2\left(x-2\right)^2\left(x-1\right)}=\frac{-8x}{\left(x-1\right)\left(x^2-4\right)}\)

b, \(\left(\frac{2x}{2x-y}-\frac{4x^2}{4x^2+4xy+y^2}\right):\left(\frac{2x}{4x^2-y^2}+\frac{1}{y-2x}\right)\)

\(=\left(\frac{2x}{2x-y}-\frac{4x^2}{\left(2x+y\right)^2}\right):\left(\frac{2x}{\left(2x-y\right)\left(2x+y\right)}-\frac{1}{2x-y}\right)\)

\(=\left(\frac{2x\left(2x+y\right)^2-4x^2\left(2x-y\right)}{\left(2x-y\right)\left(2x+y\right)^2}\right):\left(\frac{2x-\left(2x+y\right)}{\left(2x-y\right)\left(2x+y\right)}\right)\)

\(=\left(\frac{8x^3+8x^2y+2xy^2-8x^3+4x^2y}{\left(2x-y\right)\left(2x+y\right)^2}\right):\left(\frac{-y}{\left(2x-y\right)\left(2x+y\right)}\right)\)

\(=-\left(\frac{12x^2y+xy^2}{2x+y}\right)=\frac{-12x^2y-xy^2}{2x+y}\)

Bạn ghi lại đề đi, khó nhìn quá

\(\dfrac{4xy^3}{xy^2-x^2y}+\dfrac{4x^3y}{x^2y-xy^2}\)

\(=\dfrac{4xy^3-4x^3y}{xy^2-x^2y}\)

\(=\dfrac{4xy\left(y^2-x^2\right)}{xy\left(y-x\right)}\)

\(=\dfrac{4\left(y-x\right)\left(y+x\right)}{y-x}=4\left(x+y\right)\)

(4x²+2xy+y²)(2x-y)-(2x-y)(4x²-2xy+y²)

=(2x³-y³)-(2x+y)(4x²-2xy+y²)

=(2x³-y³)-(2x³+y³)

=2x³-y³-2x³+y³

=0

ta có 4 x 3 y 2   –   8 x 2 y 3   =   4 x 2 y 2 . x   –   4 x 2 y 2 . 2 y   =   4 x 2 y 2 ( x   –   2 y )    

Vậy 4x³y² – 8x²y³ = 4x²y²(x – 2y)      

Đáp án cần chọn là: C

bấm đúng cho mik đi 

( 2x + y ) ( 4x² - 2xy + y² ) - ( 2x - y ) ( 4x² + 2xy + y² )

= 8x³ + y³ - ( 8x³ - y³ )
= 2y³ 

\(\left(2x+y\right)\left(4x^2-2xy+y^2\right)-\left(2x-y\right)\left(4x^2+2xy+y^2\right)\)

\(=8x^3+y^3-\left(8x^3-y^3\right)\)

\(=8x^3+y^3-8x^3+y^3\)

\(=\left(8x^3-8x^3\right)+\left(y^3+y^3\right)\)

\(=2y^3\)

(2x + y)(4x2 – 2xy + y2) – (2x – y)(4x2 + 2xy + y2)

= (2x + y)[(2x)2 – 2x.y + y2] – (2x – y)[(2x)2 + 2x.y + y2]

= [(2x)3 + y3] – [(2x)3 – y3]

= (2x)3 + y3 – (2x)3 + y3

= 2y3

Tham khảo:

a)

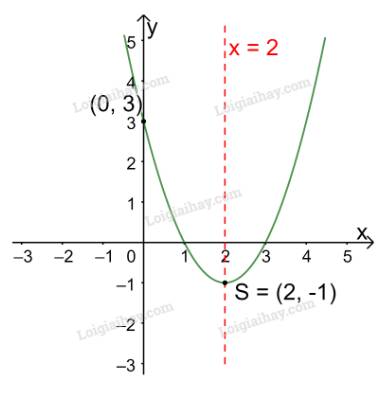
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = {x^2} - 4x + 3\) là một parabol (P):

+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - ( - 4)}}{{2.1}} = 2;{y_S} = {2^2} - 4.2 + 3 =  - 1.\)

+ Có trục đối xứng là đường thẳng \(x = 2\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);

+ Bề lõm quay lên trên vì \(a = 1 > 0\)

+ Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3).

Ta vẽ được đồ thị như hình dưới.

b)

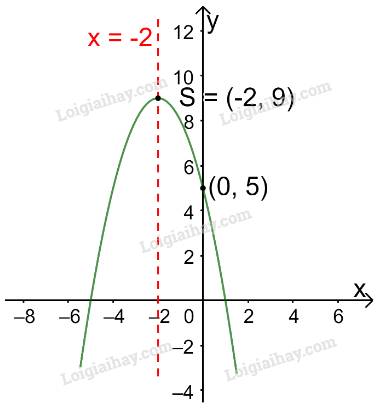
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y =  - {x^2} - 4x + 5\) là một parabol (P):

+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - ( - 4)}}{{2.( - 1)}} =  - 2;{y_S} =  - {( - 2)^2} - 4.( - 2) + 5 = 9.\)

+ Có trục đối xứng là đường thẳng \(x =  - 2\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);

+ Bề lõm quay xuống dưới vì \(a =  - 1 < 0\)

+ Cắt trục tung tại điểm có tung độ bằng 5, tức là đồ thị đi qua điểm có tọa độ (0; 5).

Ta vẽ được đồ thị như hình dưới.

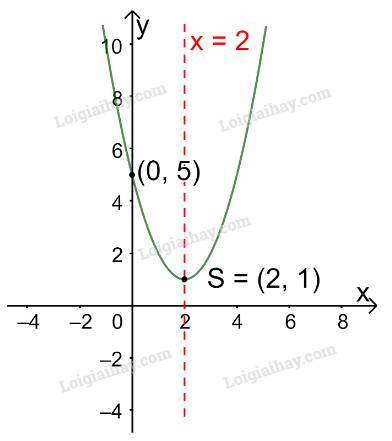
c) Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = {x^2} - 4x + 5\) là một parabol (P):

+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - ( - 4)}}{{2.1}} = 2;{y_S} = {2^2} - 4.2 + 5 = 1.\)

+ Có trục đối xứng là đường thẳng \(x = 2\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);

+ Bề lõm quay lên trên vì \(a = 1 > 0\)

+ Cắt trục tung tại điểm có tung độ bằng 5, tức là đồ thị đi qua điểm có tọa độ (0; 5).

Ta vẽ được đồ thị như hình dưới.

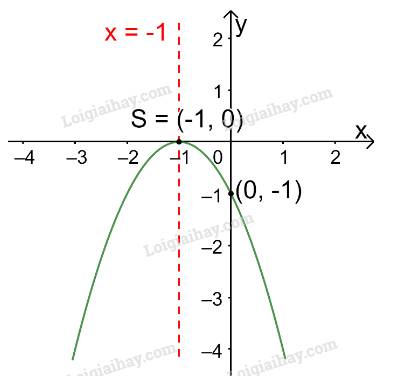
d)

Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y =  - {x^2} - 2x - 1\) là một parabol (P):

+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - ( - 2)}}{{2.( - 1)}} =  - 1;{y_S} =  - {( - 1)^2} - 2.( - 1) - 1 = 0\)

+ Có trục đối xứng là đường thẳng \(x =  - 1\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);

+ Bề lõm quay xuống dưới vì \(a =  - 1 < 0\)

+ Cắt trục tung tại điểm có tung độ bằng -1, tức là đồ thị đi qua gốc tọa độ (0; -1).

Ta vẽ được đồ thị như hình dưới.