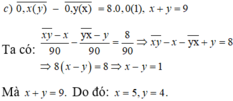Lời giải:
$\overline{0,abc}\times (a+b+c)=1$

$\overline{abc}\times (a+b+c)=1\times 1000=1000=2\times 500 = 4\times 250=5\times 200=8\times 125=10\times 100$

Vì $\overline{abc}$ là số có 3 chữ số nên $\overline{abc}$ có thể là $500, 250, 200, 125,100$

Nếu $\overline{abc}=500\Rightarrow a+b+c=5$

Ta có: $500\times 5=2500$ (loại) 

Nếu $\overline{abc}=250\Rightarrow a+b+c=7$

Ta có: $250\times 7=1750$ (loại) 

Nếu $\overline{abc}=200\Rightarrow a+b+c=2$

Ta có: $200\times 2=400$ (loại) 

Nếu $\overline{abc}=125\Rightarrow a+b+c=8$

Ta có: $125\times 8=1000$ (thỏa mãn) 

Nếu $\overline{abc}=100\Rightarrow a+b+c=1$

Ta có: $100\times 1=100$ (loại)

Vậy $\overline{abc}=125$ nên $\overline{0,abc}=0,125$

\(\overline{0,abc}\) . ( a + b + c ) = 1

=> \(\overline{abc}\) ( a + b + c ) = 1000 

Mà \(\overline{abc}\) và ( a + b + c ) là các số tự nhiên nên ( a + b + c ) và \(\overline{abc}\) là ước của 1000 = 125.8 = 200.5 = 100.10 = 500.2

Xét trong 4 trường hợp đó ta chọn 1000 = 125.8 ( Thỏa \(\overline{abc}\) = 125 ; a+b+ c = 1+2+5 = 8 và \(\overline{abc}\) .(a+b+c)=1000

Vậy \(\overline{0.abc}\) = 0.125

cảm ơn nhiều nhé

doantrancaotri cậu thật thông minh đó nha

nói thiệt cảm ơn nhiều nhiều nhiều luôn đấy

Lời giải:
$\overline{0,abc}\times (a+b+c)=1$

$\overline{abc}\times (a+b+c)=1\times 1000=1000=2\times 500 = 4\times 250=5\times 200=8\times 125=10\times 100$

Vì $\overline{abc}$ là số có 3 chữ số nên $\overline{abc}$ có thể là $500, 250, 200, 125,100$

Nếu $\overline{abc}=500\Rightarrow a+b+c=5$

Ta có: $500\times 5=2500$ (loại) 

Nếu $\overline{abc}=250\Rightarrow a+b+c=7$

Ta có: $250\times 7=1750$ (loại) 

Nếu $\overline{abc}=200\Rightarrow a+b+c=2$

Ta có: $200\times 2=400$ (loại) 

Nếu $\overline{abc}=125\Rightarrow a+b+c=8$

Ta có: $125\times 8=1000$ (thỏa mãn) 

Nếu $\overline{abc}=100\Rightarrow a+b+c=1$

Ta có: $100\times 1=100$ (loại)

Vậy $\overline{abc}=125$ nên $\overline{0,abc}=0,125$

Áp dụng bđt Cauchy cho 2 số không âm :

\(x^2+\frac{1}{x}\ge2\sqrt[2]{\frac{x^2}{x}}=2.\sqrt{x}\)

\(y^2+\frac{1}{y}\ge2\sqrt[2]{\frac{y^2}{y}}=2.\sqrt{y}\)

Cộng vế với vế ta được :

\(x^2+y^2+\frac{1}{x}+\frac{1}{y}\ge2.\sqrt{x}+2.\sqrt{y}=2\left(\sqrt{x}+\sqrt{y}\right)\)

Vậy ta có điều phải chứng mình 

Ta đi chứng minh:\(a^3+b^3\ge ab\left(a+b\right)\)

\(\Leftrightarrow\left(a-b\right)^2\left(a+b\right)\ge0\)* đúng *

Khi đó:

\(\frac{1}{a^3+b^3+abc}\le\frac{1}{ab\left(a+b\right)+abc}=\frac{1}{ab\left(a+b+c\right)}=\frac{c}{abc\left(a+b+c\right)}\)

Tương tự:

\(\frac{1}{b^3+c^3+abc}\le\frac{a}{abc\left(a+b+c\right)};\frac{1}{c^3+a^3+abc}\le\frac{b}{abc\left(a+b+c\right)}\)

\(\Rightarrow LHS\le\frac{a+b+c}{abc\left(a+b+c\right)}=\frac{1}{abc}\)

Trời ạ cay vãi shit đánh máy xong rồi tự nhiên bấm hủy T.T bài 1 ngắn đã đành ......

\(WLOG:a\ge b\ge c\)

Ta dễ có:\(\frac{a}{b+c+1}+\frac{b}{c+a+1}+\frac{c}{a+b+1}\)

\(\le\frac{a}{b+c+1}+\frac{b}{b+c+1}+\frac{c}{b+c+1}\)

\(=\frac{a+b+c}{b+c+1}\)

Ta cần chứng minh:

\(\frac{a+b+c}{b+c+1}+\left(1-a\right)\left(1-b\right)\left(1-c\right)\le1\)

\(\Leftrightarrow a+b+c+\left(1-a\right)\left(1-b\right)\left(1-c\right)\left(b+c+1\right)\le1+b+c\)

\(\Leftrightarrow\left(1-a\right)\left(1-b\right)\left(1-c\right)\left(1+b+c\right)\le1-a\) ( 1 )

Mà theo AM - GM :

\(\left(1-b\right)\left(1-c\right)\left(1+b+c\right)\le\left(\frac{1-b+1-c+1+b+c}{3}\right)^3=1\)

Khi đó ( 1 ) đúng

Vậy ta có đpcm

Nếu bài toán trở thành

\(\frac{a}{bc+2}+\frac{b}{ca+2}+\frac{c}{ab+2}+\left(1-a\right)\left(1-b\right)\left(1-c\right)\le1\) thì bài toán khó định hướng hơn rất nhiều :D

Cho abc(a+b+c) khác 0. Giải phương trình ẩn x:

(x-a)/bc+(x-b)/ac+(x-c)/ab=1/2(1/a+1/b+1/c)

.

bf