cho tam giác ABC vuông tại C, đường cao CH. Đường tròn (I; r) nội tiếp tam giác ABC tiếp xúc với AC, AB lần lượt ở P và Q. Giao điểm của CH và PQ là N. Gọi K là trung điểm của BC, KI cắt AC tại M. Chứng minh rằng CM=CN

Những câu hỏi liên quan
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$. Đường tròn tâm $I$ đường kính $BH$ cắt $AB$ tại $D$. Đường tròn $(J)$ đường kính $CH$ cắt $AC$ tại $E$. Chứng minh $DE$ là tiếp tuyến chung của đường tròn $(I)$ và đường tròn $(J)$.
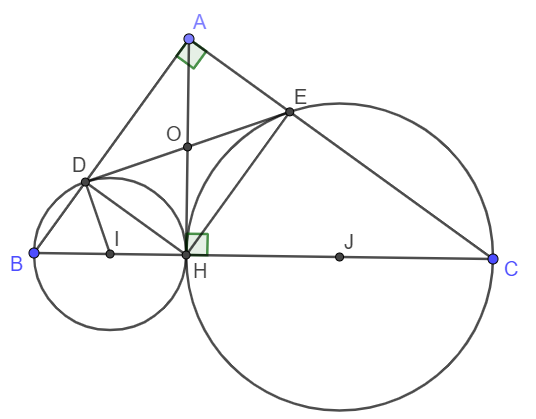
Để chứng minh DE là tiếp tuyến của đường tròn tâm I đường kính BH ta chỉ cần chứng minh ID\perp DEID⊥DE .
Vì D, E lần lượt thuộc đường tròn đường kính BH và HC nên ta có: \widehat{BDH}=\widehat{CEH}=90^oBDH=CEH=90o.
Suy ra tứ giác ADHE là hình chữ nhật.
Gọi O là giao điểm của AH và DE, khi đó ta có OD = OH = OE = OA.
Suy ra tam giác ODH cân tại O vì vậy \widehat{ODH}=\widehat{OHD}ODH=OHD.
Ta cũng có tam giác IDH cân tại I suy ra \widehat{IDH}=\widehat{IHO}IDH=IHO.
Suy ra \widehat{IDO}+\widehat{OHD}=\widehat{IHD}+\widehat{IHA}=90^oIDO+OHD=IHD+IHA=90o \Leftrightarrow\widehat{IDO}=90^o⇔IDO=90o hay DI \perp⊥ DE.
Ta có DI\perp DE\left(D\in\left(I\right)\right)DI⊥DE(D∈(I)) suy ra DE tiếp xúc với (I) tại D.
Chứng minh tương tự ta cũng có DE tiếp xúc với (J) tại E.
Vậy DE là tiếp tuyến chung của đường tròn (I) và đường tròn (J).
Vì D, E lần lượt thuộc đường tròn đường kính BH và HC nên ta có : góc BHD = góc CEH=90°
=> tứ giác ADHE là hình chữ nhật
Gọi O là giao điểm của AH và DE khi đó ta có OD=OE=OA
=> Tam giác ODH cân tại O vì vậy góc ODH = góc OHD
Ta cũng có tam giác IDH cân tại I suy ra góc IDH= góc IHO
=> góc IDO + góc OHD = góc IHD + góc IHA=90° <=> góc IDO = 90° hay DI ⊥ DE
ta có DI ⊥ DE ( D ∈ I) => DE tiếp xúc với (I) tại D
Ta có DE tiếp xúc với (J) tại E
Vậy DE là tiếp tuyến chung của đường tròn (I) và đường tròn (J)
vì D,E lần lượt thuộc đương tròn đương kính BH và CH nên ta có góc BDH =CEH =90' ⇒tứ giác ADHE là hình chữ nhật
gọi O là giao điểm của AH và DE khi đó ta có OD=OH=OE=OA
⇒ΔODH cân tại O vì vậy gcos ODH=OHD
ta cũng có tam giác IDH caantaij I suy ra góc IHD =IHO
suy ra góc IDO+OHD =IHD +IHA = 90'
⇒góc IDO =90' HAY DI vuông góc với DE
suy ra DE tiếp xúc với I tạo D và DE tiếp xúc với J tại E
vậy ED là tiếp tuyến chung của 2 đương tròn J và I
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A, đường cao AH. a) Giải tam gaics ABC biết góc B = 36 và AC =6cm b)vẽ đường tròn tâm I đường kính BH cắt AB tại M và đường tròn tâm K đường kính CH cắt AC tại N. Chứng minh tứ giác AMHN là hình chữ nhật. Tính độ dài MN. c) CHứng minh MN là tiếp tuyến chung của đường tròn (I) và (K) d) Nêu điều kiện về tam giác ABC để MN có độ dài lớn nhất
a:
Xét đường tròn đường kính HB có
ΔHMB nội tiếp đường tròn
HB là đường kính
Do đó: ΔHMB vuông tại M
Xét đường tròn đường kính HC có
ΔHNC nội tiếp đường tròn
HC là đường kính
Do đó: ΔHNC vuông tại N
Xét tứ giác AMHN có
\(\widehat{NAM}=\widehat{ANH}=\widehat{AMH}=90^0\)
nên AMHN là hình chữ nhật
b: \(BC=\sqrt{6^2+8^2}=10\)(cm)
=>AH=6*8/10=4,8(cm)
=>MN=4,8(cm)
c: góc IMN=góc IMH+góc NMH
=góc IHM+góc NAH
=góc HAC+góc HCA=90 độ
=>MN là tiếp tuyến của (I)
góc KNM=góc KNH+góc MNH
=góc KHN+góc MAH
=góc BAH+góc HBA=90 độ
=>MN là tiếp tuyến của (K)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Vẽ đường tròn tâm I đường kính BH, cắt AB ở M. Vẽ đường tròn tâm K có đường kính CH , cắt AC ở Na) Tứ giác AMHN là hình gì ?b) Chứng minh tăng MN là tiếp tuyến chung của hai đường tròn (I) và (K)c) Vẽ tiếp tuyến Ax của đường tròn ngoại tiếp tam giác ABC. CMR Ax//MN
a: Xét (I) có
ΔHMB nội tiếp
HB là đường kính
Do đó: ΔHMB vuông tại M
Xét (K) có
ΔCNH nội tiếp
CH là đường kính
=>ΔCNH vuông tại N
Xét tứ giác AMHN có
góc AMH=góc ANH=góc MAN=90 độ
nên AMHN là hình chữ nhật
b: góc NMI=góc NMH+góc IMH
=góc NAH+góc IHM
=góc CAH+góc HCA=90 độ
=>NM là tiếp tuyến của (I)
góc KNM=góc KNH+góc MNH
=góc KHN+góc MAH
=góc BAH+góc B=90 độ
=>MN là tiếp tuyến của (K)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB 4cm, AC3cm, đường cao AH. Vẽ đường tròn tâm C, bán kính CA. Đường thẳng AH cắt đường trong (C) tại điểm thứ 2 là D
Cho tam giác ABC vuông tại A có AB4cm, AC3cm, đường cao AH. Vẽ đường tròn tâm C, bán kính CA. Đường thẳng AH cắt đường trong (C) tại điểm thứ 2 là D.
a) Tính độ dài đoạn thẳng AH
b) Chứng minh BD là tiếp tuyến của đường tròn (C)
c) Qua C kẻ đường thẳng vuông góc với BC cắt các tia BA,BD thứ tự E,F. Trên cung nhỏ AD của (C) lấy điểm M bất kỳ, qua...
Đọc tiếp
Cho tam giác ABC vuông tại A có AB = 4cm, AC=3cm, đường cao AH. Vẽ đường tròn tâm C, bán kính CA. Đường thẳng AH cắt đường trong (C) tại điểm thứ 2 là D Cho tam giác ABC vuông tại A có AB=4cm, AC=3cm, đường cao AH. Vẽ đường tròn tâm C, bán kính CA. Đường thẳng AH cắt đường trong (C) tại điểm thứ 2 là D. a) Tính độ dài đoạn thẳng AH b) Chứng minh BD là tiếp tuyến của đường tròn (C) c) Qua C kẻ đường thẳng vuông góc với BC cắt các tia BA,BD thứ tự E,F. Trên cung nhỏ AD của (C) lấy điểm M bất kỳ, qua M kẻ tiếp tuyến với (C) cắt AB,BD lần lượt tại P,Q. Chứng minh EF bình phương =4PE.QF
a:\(BC=\sqrt{4^2+3^2}=5\left(cm\right)\)
AH=4*3/5=2,4cm
b: ΔCAD cân tại C
mà CH là đường cao
nên CH là phân giác của góc ACD
Xét ΔCAB và ΔCDB có
CA=CD
góc ACB=góc DCB
CB chung
Do dó: ΔCAB=ΔCDB
=>góc CDB=90 độ
=>BD là tiếp tuyến của (C)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, ∠ABC = 60◦
, AB = a.
a) Xác định tâm O và tính bán kính đường tròn ngoại tiếp tam giác ABC.
b) Vẽ đường cao AH. Đường tròn đường kính BH cắt AB tại D và đường tròn đường
kính CH cắt AC tại E. Tứ giác ADHE là hình gì? Tính DE.
c) Chứng minh rằng AO⊥DE.
a: O là trung điểm của BC
b: Xét \(\left(\dfrac{BH}{2}\right)\) có
ΔBDH là tam giác nội tiếp
BH là đường kính
Do đó: ΔBDH vuông tại D
Xét \(\left(\dfrac{CH}{2}\right)\)có
ΔCHE nội tiếp đường tròn
CH là đường kính
Do đó: ΔCHE vuông tại E
Xét tứ giác ADHE có
\(\widehat{AEH}=\widehat{ADH}=\widehat{EAD}=90^0\)
Do đó: ADHE là hình chữ nhật
Đúng 0
Bình luận (1)
2) Cho tam giác ABC vuông tại A, có đường cao AH, gọi I,J, K lần lượt là tâm đường tròn nội tiếp các tam giác ABC, AHB, AHC.
a) C/m AI vuông góc với JK
b) C/m tứ giác BJKC nội tiếp đuợc đường tròn
cho tam giác ABC vuông tại A, đường cao AH. Gọi I,J,K lần lượt là tâm đường tròn nội tiếp tam giác ABC, AHB, AHC. C/M: AI vuông góc JK .
Cho tam giác ABC vuông tại A, đường cao AH, vẽ đường tròn tâm I đươngf kính BH cắt AB tại D.Vẽ đường tròn tâm K đường kính CH cắt AC tại E. CMR:
a, AD.AB=AE.AC
b,DE là tiếp tuyến chung của đường tròn tâm I và tâm K
Cho tam giác ABC vuông tại A đường cao AH đường tròn đường kính AH cắt AB,AC tại E,F
a,c/m AEHF là hình chữ nhật
b,đường thẳng qua A vuông với EF cắt BC tại I .c/m i là trung điểm của BC
c, c/m Nếu S tam giác ABC = S hình chữ nhật AEHF thì tam giác ABC vuông cân














