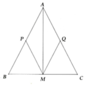
cho tam giác ABC , trung tuyến AM , qua M kẻ đường thẳng song song với AC cắt AB ở P. qua M kẻ đường thẳng song song với AB cắt AC ở Q.
a) tu giac APMQ là hình gì , vì sao?
b) tam giacABC cần điều kiện gì thì APMQ là hình chữ nhật?
c)_____________________________________hình thoi?