Cho AB và CD là 2 đoạn thẳng song song và bằng nhau,A`B`và C`D`là các hình chiếu của chúng trên cùng 1 dường thẳng.Chứng minh A`B`=C`D`

Những câu hỏi liên quan
Cho AB và CD là hai đoạn thẳng song song và bằng nhau. MN và PQ là các hình
chiếu của chúng trên cùng một đường thẳng khác. Chứng minh MN= PQ.
Cho AB và CD là hai đoạn thẳng song song và bằng nhau , A'B' và C'D' là hình chiếu của chúng trên cùng 1 đường thẳng . CM A'B'=C'D'
Cho AB và CD là hai đoạn thẳng song song và bằng nhau, A'B' và C'D' là các hình chiếu của chúng trên cùng một đường thẳng. Chứng minh rằng A'B' = C'D'
GIÚP MK VS NHA. CẢM ƠN MỌI NGƯỜI NHIỀU Ạ
@soyeon_Tiểubàng giải
1 câu trả lời
Toán lớp 7 Ôn tập toán 7

Từ A hạ đường vuông góc với BB' tại H
Từ C hạ đường vuông góc với DD' tại K
Gọi I là giao điểm của CD và BB'
Dễ thấy BB' // DD' do cùng _|_ A'D'
=> BID = IDK (so le trong)
Lại có: ABI = BID (so le trong)
=> IDK = ABI
Xét t/g ABH vuông tại H và t/g CDK vuông tại K có:
AB = CD (gt)
ABH = CDK (cmt)
Do đó, t/g ABH = t/g CDK ( cạnh huyền - góc nhọn)
=> AH = CK (2 cạnh tương ứng) (1)
Có: AH // A'B' ( cùng _|_ BB')
AA' // B'H ( cùng _|_ A'D')
=> AH = A'B' ( tính chất đoạn chắn) (2)
Tương tự ta cũng có: CK = C'D' (3)
Từ (1); (2) và (3) => A'B' = C'D' (đpcm)
Đúng 0
Bình luận (0)
Bài này có trong câu hỏi tương tự bạn nên tìm nhé :)))
Mình dán lên đây cho bạn xem cho tiện
Đúng 0
Bình luận (0)
cho tam giác ABC vuông cân tại A. Gọi E và F là các hình chiếu của B và C trên xy.
a, Chứng minh CF bằng hình chiếu của A, B trên xy
b, chứng minh khi xy song song với BC thì các hình chiếu của AB và AC trên xy bằng nhau
c, Đường thẳng xy phải có điều kiện gì để các hình chiếu của AB và AC trên xy trùng nhau
(Thừa Thiên Huế - 2020)
Cho đường tròn tâm $O$ đường kính $AB$. Trên đường tròn $(O)$ lấy điểm $C$ không trùng $B$ sao cho $AC BC$. Các tiếp tuyến của đường tròn $(O)$ tại $A$ và tại $C$ cắt nhau tại $D$. Gọi $H$ là hình chiếu vuông góc của $C$ trên $AB$, $E$ là giao điểm của hai đường thẳng $OD$ và $AC$.
a. Chứng minh $OECH$ là tứ giác nội tiếp.
b. Gọi $F$ là giao điểm của hai đường thẳng $CD$ và $AB$. Chứng minh $2widehat{BCF} + widehat{CFB} 90^{circ}$.
c. Gọi $M$ là giao điểm của hai đư...
Đọc tiếp
(Thừa Thiên Huế - 2020)
Cho đường tròn tâm $O$ đường kính $AB$. Trên đường tròn $(O)$ lấy điểm $C$ không trùng $B$ sao cho $AC > BC$. Các tiếp tuyến của đường tròn $(O)$ tại $A$ và tại $C$ cắt nhau tại $D$. Gọi $H$ là hình chiếu vuông góc của $C$ trên $AB$, $E$ là giao điểm của hai đường thẳng $OD$ và $AC$.
a. Chứng minh $OECH$ là tứ giác nội tiếp.
b. Gọi $F$ là giao điểm của hai đường thẳng $CD$ và $AB$. Chứng minh $2\widehat{BCF} + \widehat{CFB} = 90^{\circ}$.
c. Gọi $M$ là giao điểm của hai đường thẳng $BD$ và $CH$. Chứng minh hai đường thẳng $EM$ và $AB$ song song với nhau.
DC = DA
OA = OC
Do đó OD là trung trực của đoạn thẳng AC : suy ra OD vuông góc với AC
Tứ giác OECH có góc CEO + góc CHO = 180 độ
Suy ra tứ giác OECH là tứ giác nội tiếp
Trên cung nhỏ
A
B
⏜
của (O), cho hai điểm C và D sao cho cung
A
B
⏜
được chia thành ba cung bằng nhau (
A
C
⏜
C
D
⏜
D...
Đọc tiếp
Trên cung nhỏ A B ⏜ của (O), cho hai điểm C và D sao cho cung A B ⏜ được chia thành ba cung bằng nhau ( A C ⏜ = C D ⏜ = D B ⏜ ). Bán kính OC và OD cắt dây AB lần lượt tại E và F
a, Hãy so sánh các đoạn thẳng AE và FB
b, Chứng minh các đường thẳng AB và CD song song
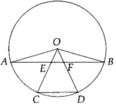
a, Chứng minh được ∆OEA = ∆OFB => AE = FB
b, Chứng minh được O E F ^ = O C D ^ => AB//CD
Đúng 0
Bình luận (0)
Bài 19: Cho tam giác ABC có AC > AB. M là một điểm bất kỳ trên cạnh BC. Tìm vị trí
điểm M sao cho AM có độ dài nhỏ nhất.
Bài 20: Cho AB và CD là hai đoạn thẳng song song và bằng nhau. MN và PQ là các hình
chiếu của chúng trên cùng một đường thẳng khác. Chứng minh MN PQ.
Bài 21: Cho tam giác ABC vuông tại A, kẻ AH vuông góc BC ( H BC). Chứng minh:
AH + BC > AB + AC.
bài 4 cho đoạn thẳng AB và đường thẳng d song song với AB và C là điểm bất kì thuộc đường thẳng d . Gọi M , N, P lần lượt là trung điểm của các cạnh BC,AC,AB và G là giao điểm của AM , BN
a, chứng minh các điểm C ,G,P thẳng hàng
b, khi C di chuyển trên dường thẳng d thì điểm G di chuyển trên đường thẳng nào .
Tam giác ABC vuông cân tại A, xy bất kỳ đi qua A, gọi EF là hình chiếu của BC trên xy.
a. Chứng minh CF bằng hình chiếu của AB trên xy.
b. Chứng minh khi xy song song BC thì các hình chiếu của AB và AC trên xy bằng nhau.
c. Đường thẳng xy phải có điều kiện gì để các hình chiếu của AB và AC trên xy trùng nhau
Cho ∆ABC.D là điểm trên đường thẳng qua A song song với BC sao cho C,D nằm cùng phía với AB và AD = BC a)Chứng minh rằng AB // CD b)Gọi M là trung điểm của AC.Trên các đoạn AD,BC lần lượt I,K sao cho AI = CK.Chứng minh rằng I,M,K thẳng hàng.
a: Xét tứ giác ABCD có
AD//BC
AD=BC
Do đó: ABCD là hình bình hành
Suy ra: AB//CD
Đúng 0
Bình luận (0)


















