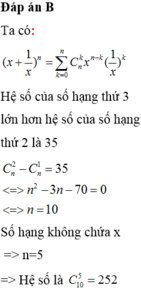Trong khai triển của , hệ số của x là gì

Những câu hỏi liên quan
15. Số hạng chính giữa trong khai triển (3x + 2y)^4 là?
18. Tìm hệ số của x^7 trong khai triển : h(x)= x(2 + 3x)^9 là?
19. Tìm hệ số của x^7 trong khai triển g(x)= (1+x)^7 + (1-x)^8 + (2+x)^9 là?
15/ Mũ 4=> có 4+1=5 số hạng=> số hạng chính giữa là: \(C^2_4.3^{4-2}.x^2.2^2y^2=58x^2y^2\)
18/ \(x.x^k=x^7\Rightarrow k=6\)
\(C^6_9.3^6.2^3=489888\)
19/ \(C^7_7+C^7_8.\left(-1\right)^7+C^7_9.2^2=...\)
Đúng 1
Bình luận (3)
trong biểu thức khai triển của (1-x)6 , hệ số của số hạng chứa x3 là gì ?
Cho n là số nguyên dương sao cho tổng các hệ số trong khai triển của x + 1 n bằng 1024. Hệ số của x 8 trong khai triển đó bằng
A. 2 8
B. 90
C. 45
D. 80
Trong khai triển nhị thức
x
+
1
x
n
,
x
≠
0
, hệ số của số hạng thứ 3 lớn hơn hệ số của số hạng thứ 2 là 35. Tìm số hạng không chứa x trong khai triển nói trên. A. 225 B. 252 C. 522 D. 525
Đọc tiếp
Trong khai triển nhị thức x + 1 x n , x ≠ 0 , hệ số của số hạng thứ 3 lớn hơn hệ số của số hạng thứ 2 là 35. Tìm số hạng không chứa x trong khai triển nói trên.
A. 225
B. 252
C. 522
D. 525
Trong khai triển nhị thức
x
+
1
x
n
,
x
≠
0
hệ số của số hạng thứ 3 lớn hơn hệ số của số hạng thứ 2 là 35. Tìm số hạng không chứa x trong khai triển nói trên. A. 225 B. 252 C. 522 D. 525
Đọc tiếp
Trong khai triển nhị thức x + 1 x n , x ≠ 0 hệ số của số hạng thứ 3 lớn hơn hệ số của số hạng thứ 2 là 35. Tìm số hạng không chứa x trong khai triển nói trên.
A. 225
B. 252
C. 522
D. 525
Trong khai triển nhị thức ( x + 1 x ) n hệ số của số hạng thứ 3 lớn hơn hệ số của số hạng thứ 2 là 35. Tìm số hạng không chứa x trong khai triển nói trên.
A. 225
B. 252
C. 522
D. 525
1. Tìm hệ số của số hạng x^4 trong khai triển left(x-3right)^92. Tìm hệ số của số hạng chứa x^{12}y^{13} trong khai triển left(2x+3yright)^{25}3. Tìm hệ số của số hạng chứa x^4 trong khai triển left(dfrac{x}{3}-dfrac{3}{x}right)^{12}4. Tìm hệ số của số hạng không chứa x trong khai triển left(x^2-dfrac{1}{x}right)^65. Tìm hệ số của số hạng không chứa x trong khai triển left(x+dfrac{1}{x^4}right)^{10}
Đọc tiếp
1. Tìm hệ số của số hạng \(x^4\) trong khai triển \(\left(x-3\right)^9\)
2. Tìm hệ số của số hạng chứa \(x^{12}y^{13}\) trong khai triển \(\left(2x+3y\right)^{25}\)
3. Tìm hệ số của số hạng chứa \(x^4\) trong khai triển \(\left(\dfrac{x}{3}-\dfrac{3}{x}\right)^{12}\)
4. Tìm hệ số của số hạng không chứa x trong khai triển \(\left(x^2-\dfrac{1}{x}\right)^6\)
5. Tìm hệ số của số hạng không chứa x trong khai triển \(\left(x+\dfrac{1}{x^4}\right)^{10}\)
Biết rằng trong khai triển trên tổng hệ số của ba số hạng đầu bằng 161. Tìm a Gọi x là hệ số không chứa x trong khai triển nhị thức Niu – tơn
x
2
-
2
x
n
C
n
0...
Đọc tiếp
Biết rằng trong khai triển trên tổng hệ số của ba số hạng đầu bằng 161. Tìm a
Gọi x là hệ số không chứa x trong khai triển nhị thức Niu – tơn
x 2 - 2 x n = C n 0 x 2 n + C n 1 x 2 n - 1 - 2 x + . . . + C n n - 1 x 2 - 2 x n - 1 + C n n - 2 x n n ∈ ℕ *
Biết rằng trong khai triển trên tổng hệ số của ba số hạng đầu bằng 161. Tìm a
A. 11520
B. 11250
C. 12150
D. 10125
Biết rằng trong khai triển nhị thức Newton của
x
+
1
x
n
tổng các hệ số của hai số hạng đầu bằng 24. Gọi S là tổng các hệ số của số hạng chứa
x
k
k
0
. Hỏi S có tính chất gì trong các tính chất sau? A. S là một số nguyên tố. B. S...
Đọc tiếp
Biết rằng trong khai triển nhị thức Newton của x + 1 x n tổng các hệ số của hai số hạng đầu bằng 24. Gọi S là tổng các hệ số của số hạng chứa x k k > 0 . Hỏi S có tính chất gì trong các tính chất sau?
A. S là một số nguyên tố.
B. S là một lũy thừa của 24
C. S là một số chính phương
D. S là một số lập phương đúng.
Ta có x + 1 x n = ∑ k = 0 n C n k x n - 2 k
Theo đề ta có C n 0 + C n 1 = 24 ⇔ 1 + n = 24 ⇔ n = 23
Số hạng chứa x mũ nguyên dương thỏa n - 2 k > 0 ⇔ k < n 2 = 23 2
Do k ∈ Z nên k ∈ 1 ; 2 ; 3 ; . . 11 .
Suy ra có 12 số hạng chứa x mũ nguyên dương
Đáp án C
Đúng 0
Bình luận (0)