cho tam giác abc, trên ab và ac lần lượt lấy hai điểm d và e, sao cho ad=1/2 ab, ae=1/2 ec. tính tam giác abc

Những câu hỏi liên quan
Cho Hình Tam Giác ABC, trên AB và AC lần lượt lấy điểm D và E sao cho AD = DB, AE = 1/3 EC ; CD cắt BE tại O. Tính diện tích Hình Tam Giác ABC biết diện tích Tam Giác BDO là 20cm2.
Bài 1: Tam giác ABC có diện tích là 180m 2 , D là điểm chính giữa AB . Trên AC lấy điểm E sao cho AE bằng 1/3 EC. Tính diện tích tam giác AED Bài 2: Cho tam giác ABC , Trên AB lấy điểm D,E sao cho AD DE EB . Trên AC lấy điểm H, K sao cho AH HK KC . Trên BC lấy M,N sao cho BM MN NC . Tính diện tích DEMNKH . Biết diện tích tạm giác ABC là 270 cm2.Bài 3: Cho tam giác ABC , Điểm D nằm trên cạnh AC , điểm E nằm trên cạnh BC sao cho : AD DC , BE 3/2 EC . Các đoạn thẳng AE và BD cắt nhau AE và...
Đọc tiếp
Bài 1: Tam giác ABC có diện tích là 180m 2 , D là điểm chính giữa AB . Trên AC lấy điểm E sao cho AE bằng 1/3 EC. Tính diện tích tam giác AED
Bài 2: Cho tam giác ABC , Trên AB lấy điểm D,E sao cho AD = DE = EB . Trên AC lấy điểm H, K sao cho AH = HK = KC . Trên BC lấy M,N sao cho BM = MN = NC . Tính diện tích DEMNKH . Biết diện tích tạm giác ABC là 270 cm2.
Bài 3: Cho tam giác ABC , Điểm D nằm trên cạnh AC , điểm E nằm trên cạnh BC sao cho : AD = DC , BE = 3/2 EC . Các đoạn thẳng AE và BD cắt nhau AE và BD cắt nhau ở K .
a, BK gấp mấy lần KD.
b, Biết diện tích tam giác ABC bằng 80m2. Tính diện tích hình DKEC
Mình học lớp 5 mà chưa học bài này
cô ra thêm bài khó trong giờ học cho mấy bạn giỏi có cái mà làm
Đúng 0
Bình luận (0)
Bài 1 : Tam giác ABC có 3 đường phân giác AD, BE, CF. Cm :
a, DB/DC.EC/EA.FA/FB=1
b, 1/AD+1/BE+1/CF>1/BC+1/CA+1/AB
Bài 2: Cho tam giác ABC, trên BC, AC lần lượt lấy D và E sao cho BD/BC=3/7, AE/EC=2/5A. Gọi I là giao điểm của AD và BE. Tính tỉ số AI/ID
Bài 3 : Cho tam giác ABC có AB < AC, D và E là các điểm trên AB, AC sao cho BD = CE, DE cắt BC tại K. Cm : AB/AC=KE/KD
Cho tam gíac ABC, trên AB và AC, lần lượt lấy E và D sao cho AE/AC = AD/AB = 1/3
a, chứng minh tam giác ADE ~ tam giác ABC
b, gọi I là giao điểm của BD và EC. Chứng minh ID.IB = IE.IC
Bài 1: 1) Trên tia Ax lấy các điểm B, C, D theo thứ tự đó đó sao cho cho: AB 2 cm, BC 4 cm và CD 8 cm.a) Tính các tỷ số số AB/ BC và BC/CDb) Chứng minh BC2 AB.CD2) Trên đường thẳng d , lấy 4 điểm A, B, C, D theo thứ tự đó sao cho cho AB/BC 3/5, BC/CD 5/6.a) Tính tỉ số AB/CDb) Cho biết AD 28 cm. Tính độ dài các đoạn thẳng AB, BC và CD Bài 2: Cho tam giác ABC và các điểm D, E lần lượt nằm trên hai cạnh AB, AC sao cho AD/AB AE/AC.a) Chứng minh AD/BD AE/ECb) Cho biết AD 2 cm, BD 1 cm và...
Đọc tiếp
Bài 1: 1) Trên tia Ax lấy các điểm B, C, D theo thứ tự đó đó sao cho cho: AB = 2 cm, BC = 4 cm và CD = 8 cm.
a) Tính các tỷ số số AB/ BC và BC/CD
b) Chứng minh BC2 = AB.CD
2) Trên đường thẳng d , lấy 4 điểm A, B, C, D theo thứ tự đó sao cho cho AB/BC = 3/5, BC/CD = 5/6.
a) Tính tỉ số AB/CD
b) Cho biết AD = 28 cm. Tính độ dài các đoạn thẳng AB, BC và CD
Bài 2: Cho tam giác ABC và các điểm D, E lần lượt nằm trên hai cạnh AB, AC sao cho AD/AB = AE/AC.
a) Chứng minh AD/BD = AE/EC
b) Cho biết AD = 2 cm, BD =1 cm và AE = 4 cm. Tính AC.
Bài 3: Cho tam giác ABC có D, E lần lượt thuộc các cạnh AB và AC sao cho BD/AB = CE/CA.
a) Chứng minh AD/AB = AE/AC
b) Cho biết AD = 2 cm, BD = 1 cm và AC = 4 cm. Tính EC
Bài 4: Cho tam giác ACE có AC = 11 cm. Lấy điểm B trên cạnh AC sao cho BC = 6cm. Lấy điểm D trên cạnh AE sao cho BD song song với EC. Giả sử AE + ED = 25,5 cm. Hãy tính:
a) Tỷ số DE/AE
b) Độ dài các đoạn thẳng AE, DE và AD.
Bài 5: Cho tam giác ABC và điểm D trên cạnh BC sao cho BD/BC = 3/4, điểm E trên đoạn thẳng AD sao cho cho AE/AD = 1/3. Gọi K là giao điểm của BE và AC. a) Tính tỷ số số AK/KC
b) Vẽ hình bình hành ABCM. Trên cạnh MC lấy điểm G sao cho MG= 1/4 MC. Gọi N là giao điểm của AG và BM. Tính tỉ số MN/MB.
Cho tam giác ABC cân tại A,trên cạnh AB và AC lần lượt lấy điểm D và E sao cho AD AE. Gọi K là giao điểm của CD và BECho tam giác ABC cân tại A,trên cạnh AB và AC lần lượt lấy điểm D và E sao cho ADAE.Gọi K là giao điểm của CD và BE.a,Cm: tam giác ADC tam giác AEBb,Cm:tam giác KBC cânc,trên tia đối của tia CB lấy điểm M sao cho CMCBTính góc ABC nếu BAC2*góc MAC
Đọc tiếp
Cho tam giác ABC cân tại A,trên cạnh AB và AC lần lượt lấy điểm D và E sao cho AD = AE. Gọi K là giao điểm của CD và BE
Cho tam giác ABC cân tại A,trên cạnh AB và AC lần lượt lấy điểm D và E sao cho AD=AE.Gọi K là giao điểm của CD và BE.
a,Cm: tam giác ADC= tam giác AEB
b,Cm:tam giác KBC cân
c,trên tia đối của tia CB lấy điểm M sao cho CM=CB
Tính góc ABC nếu BAC=2*góc MAC
a: Xét ΔADC và ΔAEB có
AD=AE
góc DAC chung
AC=AB
=>ΔADC=ΔAEB
b: AD+DB=AB
AE+EC=AC
mà AB=AC và AD=AE
nên DB=EC
Xét ΔDBC và ΔECB có
DB=EC
góc DBC=góc ECB
BC chung
=>ΔDBC=ΔECB
=>góc KBC=góc KCB
=>ΔKBC cân tại K
Đúng 1
Bình luận (1)
1. Cho bốn điểm A, B, C, D sao cho AB//CD và AD//BC. Chứng minh tam giác ABC = tam giác CDA.
2. Cho bốn điểm A, B, C, D sao cho AB//CD và AD//BC. Chứng minh AB = CD.
3. Cho tam giác ABC. Trên các tia đối AB, AC lần lượt lấy các điểm E, F sao cho AE = AC, AF = AC. Chứng minh tam giác ABC = tam giác AFE.
1) Ta có hình vẽ sau:
Vì AB // CD nên \(\widehat{A_1}\) = \(\widehat{C_1}\) (so le trong)
AD // BC nên \(\widehat{A_2}\) = \(\widehat{C_2}\) ( so le trong)
Xét ΔABC và ΔCDA có:
\(\widehat{A_1}\) = \(\widehat{C_1}\) (cm trên)
AC: Cạnh chung
\(\widehat{A_2}\) = \(\widehat{C_2}\) (cm trên)
\(\Rightarrow\) ΔABC = ΔCDA (g.c.g) (đpcm)
2) Chứng minh tương tự ta có: ΔCDA = ABC (g.c.g)
\(\Rightarrow\) AB = CD ( 2 cạnh tương ứng) (đpcm)
3) Mình sửa lại chỗ AE = AC là AE = AB đó nha, bn ghi nhầm đề!!!
Ta có hình vẽ sau:
Xét ΔABC và ΔAFE có:
AE = AB (gt)
\(\widehat{A_1}\) = \(\widehat{A_2}\) (đối đỉnh)
AF = AC (gt)
\(\Rightarrow\) ΔABC = ΔAFE(c.g.c) (đpcm)
Đúng 0
Bình luận (0)
Bạn áp dụng trường hợp bằng nhau cạnh - góc - cạnh của tam giác rồi chứng minh nha
Đúng 0
Bình luận (0)
Bài 1 : Cho tam giác ABC . Trên cạnh AB lấy điểm D sao cho AD = 2 lần BD . Trên cạnh AC lấy điểm E sao cho AE = 2 lần EC . Nối CD , BE BE cắt CD ở G . So sánh diện tích tam giác BDG và diện tích tam giác ECG
Nối CM
Xét tam giác ACD và tam giác BCD có chung đường cao hạ từ đỉnh C xuống cạnh AB và có AD = 2 BD
=> S ACD = 2 S BCD (1)
Xét tam giác ADG và tam giác BDG có chung đường cao hạ từ đỉnh G xuống cạnh AB và có AD = 2 BD
=> S ADG = 2 S BDG (2)
Ta có : S ACG + S ADG = S ADC (3)
S BDG + S BGC = S BCD (4)
Từ (1), (2), (3) , (4) ta có :
S ACG + S AD = 2. ( S BDG + S BGC )
S ACG + 2 S BDG = 2 S BDG + 2 S BGC
=> S ACG = 2 S BCG
Vậy diện tích tam giác ACG gấp 2 lần diện tích tam giác BCG
Đúng 0
Bình luận (0)
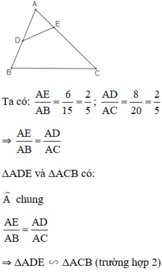
Cho tam giác ABC, trong đó AB = 15cm, AC = 20cm. Trên hai cạnh AB và AC lần lượt lấy hai điểm D và E sao cho AD = 8cm, AE = 6cm. Hai tam giác ABC và ADE có đồng dạng với nhau không? Vì sao?