Xét:

1.Nếu \(x=2016\)hoặc \(x=2017\)thì thỏa mãn đề bài

2. Nếu \(x< 2016\)thì l\(x-2016\)l\(^{2016}\)>0, lx-2017l\(^{2017}\)>1

=>lx-2016l\(^{2016}\)+lx-2017l\(^{2017}\)>1 => vô nghiệm 

3.Nếu x>2017 thì lx-2016l\(^{2016}\)>1,lx-2017l\(^{2017}\)>0

=>lx-2016l\(^{2016}\)+lx-2017l\(^{2017}\)>1=> vô nghiệm

Vậy phương trình có 2 nghiệm là ..................

\(\left|x-2015\right|^{2016}+\left|x-2016\right|^{2017}=1\)

Có: \(\left|x-2015\right|^{2016}\ge0;\left|x-2016\right|^{2017}\ge0\)

TH1: \(\hept{\begin{cases}\left|x-2015\right|^{2016}=1\\\left|x-2016\right|^{2017}=0\end{cases}}\Rightarrow\hept{\begin{cases}\left|x-2015\right|=1\\\left|x-2016\right|=0\end{cases}}\)

THa: \(x-2015=-1\Rightarrow x=2014\)

Thay vào: \(2014-2016\ne0\) ( loại)

THb: \(x-2015=1\Rightarrow x=2016\)

Thay vào:  \(2016-2016=0\)( chọn )

TH2: \(\hept{\begin{cases}\left|x-2015\right|^{2016}=0\\\left|x-2016\right|^{2017}=1\end{cases}}\Rightarrow\hept{\begin{cases}\left|x-2015\right|=0\\\left|x-2016\right|=1\end{cases}}\)

THc: \(x-2016=-1\Rightarrow x=2015\)

Thay vào:  \(2015-2015=0\)( chọn )

THd: \(x-2016=1\Rightarrow x=2017\)

Thay vào: \(2017-2015\ne0\)

Vậy: x = 2016 hoặc x = 2015

x=2015

\(\left|x-2015\right|^{2016}\ge0\)

\(\left|x-2016\right|^{2017}\ge0\)

\(\Rightarrow\orbr{\begin{cases}x=2015\\x=2016\end{cases}}\)

Lời giải:

a.

PT $\Leftrightarrow (x+3)^2=2016^{2020}-17^{91}+9$

Ta thấy: $2016^{2020}-17^{91}+9\equiv 0-(-1)^{91}+0\equiv -1\equiv 2\pmod 3$

Mà 1 scp thì chia $3$ chỉ dư $0$ hoặc $1$ nên pt vô nghiệm.

b.

$x^2=2016(y-1)^2-2017^{2019}\equiv 0-1^{2019}\equiv 3\pmod 4$
Mà 1 scp chia $4$ chỉ dư $0$ hoặc $1$ nên vô lý.

Vậy pt vô nghiệm.

c.

$(x-1)^2=2017^{2017}+1\equiv 1^{2017}+1\equiv 2\pmod 4$
Mà 1 scp khi chia cho $4$ chỉ dư $0$ hoặc $1$ nên vô lý

Vậy pt vô nghiệm

d.

$(x+2)^2=2018^{10}+4\equiv (-1)^{10}+1\equiv 2\pmod 3$

Mà 1 scp khi chia $3$ dư $0$ hoặc $1$ nên vô lý

Vậy pt vô nghiệm.

a, TK: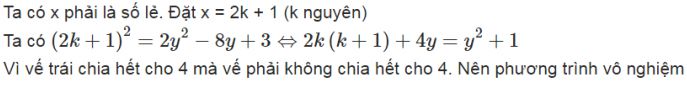

(x lẻ do \(2y^2-8y+3=2\left(y^2-4y\right)+3=x^2\) lẻ)

\(b,\Leftrightarrow\left(x^2-4x+4\right)+\left(y^2+4y+4\right)=9\\ \Leftrightarrow\left(x-2\right)^2+\left(y+2\right)^2=9\)

Vậy pt vô nghiệm do 9 ko phải tổng 2 số chính phương

|x-2016|²⁰¹⁶+|x-2017|²⁰¹⁶=1

|x-2016|²⁰¹⁶=1 hoặc |x-2017|²⁰¹⁶=1

th1:|x-2016|²⁰¹⁶=1                                                    

|x-2016|²⁰¹⁶=1²⁰¹⁶                                                                       

x-2016=1

x=1+2016

x=2017 

th2:

làm tương tự

x=2016hoac x=2017