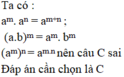Tìm các số hữu tỉ m và n; biết rằng hiệu của n và m bằng thương của n và m và bằng hai lần tổng của n và m.

Những câu hỏi liên quan
Tìm các số nguyên m để hai số hữu tỉ m+2/5 và m-5/-6 đều là số hữu tỉ dương
Để 2 số hữu tỉ đều là dương :
\(\dfrac{m+2}{5}>0\Rightarrow m>-2\left(1\right)\)
\(\dfrac{m-5}{-6}>0\Rightarrow\dfrac{5-m}{6}>0\Rightarrow m< 5\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow-2< m< 5\Rightarrow m\in\left\{-1;0;1;2;3;4\right\}\left(m\in Z\right)\)
Đúng 2
Bình luận (0)
Tìm hai số hữu tỉ m và n biết m + n = m * n = m : n
m + n = m.n => m = m.n - n = n(m - 1)
Thay m = n(m - 1) vào m + n = m: n ta có:
\(m+n=\frac{n\left(m-1\right)}{n}=m-1\)
=> m + n = m - 1=> m + n - m = -1 => n = -1
Ta có m +n = m.n => m + - 1 = - 1 .m => m - 1 = -m => m + m = 1 => 2m = 1 => m =1/2
Vậy n = -1 và m= 1/2
Đúng 0
Bình luận (0)
Tìm hai số hữu tỉ m và n Biết m + n = m * n = m : n
m + n = m.n => m = m.n - n = n(m - 1)
Thay m = n(m - 1) vào m + n = m: n ta có:
\(m+n=\frac{n\left(m-1\right)}{n}=m-1\)
=> m + n = m - 1=> m + n - m = -1 => n = -1
Ta có m +n = m.n => m + - 1 = - 1 .m => m - 1 = -m => m + m = 1 => 2m = 1 => m =1/2
Vậy n = -1 và m= 1/2
Đúng 0
Bình luận (0)
Tìm ba cách viết số hữu tỉ
-8/15
dưới dạng.
a)Tổng của hai số hữu tỉ âm. b) Hiệu của hai số hữu tỉ dương.
c) Tổng của một số hữu tỉ âm và một số hữu tỉ dương.
d) Hiệu của một số hữu tỉ âm và một số hữu tỉ dương.
:)) tui lớp 7 nha các người,mong các người đẹp zai xinh gái giúp tôi với nha các người:>
a: \(\dfrac{-8}{15}=\dfrac{-2}{15}+\dfrac{-6}{15}\)
\(\dfrac{-8}{15}=\dfrac{-1}{15}+\dfrac{-7}{15}\)
\(\dfrac{-8}{15}=\dfrac{-4}{15}+\dfrac{-4}{15}\)
b: \(-\dfrac{8}{15}=\dfrac{17}{15}-\dfrac{25}{15}\)
\(\dfrac{-8}{15}=\dfrac{9}{15}-\dfrac{17}{15}\)
\(\dfrac{-8}{15}=\dfrac{10}{15}-\dfrac{18}{15}\)
Đúng 1
Bình luận (1)
Cho số hữu tỉ \(x=\frac{3}{-7}\)
a) Tìm các số hữu tỉ y, z bằng số hữu tỉ x mà có mẫu theo thứ tự là 35; -42.
b) Tìm số hữu tỉ bằng số hữu tỉ x mà có tổng của tử và mẫu là -8
c) Tìm số hữu tỉ bằng số hữu tỉ x mà có hiệu của tử với mẫu là 30.
cho các phương trình x^2+mx+ n và x^2+px+q trong đó m,n,p,q là các số hữu tỉ sao cho (m-p)^2+(n-q)^2 > 0. Chứng minh rằng nếu hai phương trình có một nghiệm chung thì các nghiệm còn lại của hai phương trình là hai số hữu tỉ phân biệt
cho các phương trình x^2+mx+n và x^2+px+q trong đó m,n,p,q là các số hữu tỉ sao cho (m-p)^2+(n-q)^2 > 0. Chứng minh rằng nếu hai phương trình có một nghiệm chung thì các nghiệm còn lại của hai phương trình là hai số hữu tỉ phân biệt
cho các phương trình x^2+mx+ n và x^2+px+q trong đó m,n,p,q là các số hữu tỉ sao cho (m-p)^2+(n-q)^2 > 0. Chứng minh rằng nếu hai phương trình có một nghiệm chung thì các nghiệm còn lại của hai phương trình là hai số hữu tỉ phân biệt
Chọn câu sai. Với hai số hữu tỉ a,b và các số tự nhiên m,n ta có: A.
a
m
.
a
n
a
m
+
n
B.
a
.
b
m...
Đọc tiếp
Chọn câu sai. Với hai số hữu tỉ a,b và các số tự nhiên m,n ta có:
A. a m . a n = a m + n
B. a . b m = a m . b m
C. a m n = a m + n
D. a m n = a m . n