cho hình thoi abcd có góc A = 60 tính tỉ số \(\frac{AC^2}{AB^2}\)

Những câu hỏi liên quan
Cho hình thoi ABCD có A=60 tính tỉ số \(\frac{AC^2}{AB^2}\)
Cho hình thoi ABCD cạnh a, góc A=60°. Gọi E ,F lần lượt là trung điểm của các cạnh AD và CD
1, tính s tam giác BEF
2, gọi M là hình chiếu của E trên AC. I và K lần lượt là giao điểm của AC và EF với BD. Tính tỉ số MC trên EF
GIÚP MÌNH VỚI NHA!!! LÀM ƠN!
Cho hình thoi ABCD có góc A = 60o. Hãy tính tỉ số \(\frac{AC^2}{AB^2}\)
Gọi giao điểm hai đường chéo hình thoi là I
Vì hình thoi có góc A =60 nên tam giác ABD đều => AB = AD = DB
Ta có AC = 2AI
\(AI^2=AB^2-BI^2=AB^2-\frac{BD^2}{4}=AB^2-\frac{AB^2}{4}=\frac{3AB^2}{4}\)
\(\Rightarrow\frac{AC^2}{AB^2}=\frac{4AI^2}{AB^2}=\frac{4\frac{3AB^2}{4}}{AB^2}=3\)
Đúng 0
Bình luận (0)
bn giỏi thật nhưng mk có chỗ ko hỉu!!!
56657675684462454363462456346457474627685
Đúng 0
Bình luận (0)
Cho hình thoi ABCD có góc A=60 độ.Chứng minh AC^2/AB^2=3
Cho hình hộp đứng ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a và góc
B
A
D
^
60
°
,
AB’ hợp với đáy (ABCD) một góc
30
°
.
Thể tích khối hộp là: A.
a
3
2
B.
a
3...
Đọc tiếp
Cho hình hộp đứng ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a và góc B A D ^ = 60 ° , AB’ hợp với đáy (ABCD) một góc 30 ° . Thể tích khối hộp là:
A. a 3 2
B. a 3 6
C. 3 a 3 2
D. a 3 3 6
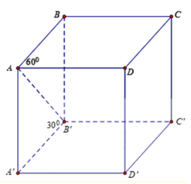
ĐÁP ÁN A
Ta có
S A B C D = a 2 sin 60 ° = a 2 3 2 A A ' = 30 ° = a 3 3
Thể tích khối hộp là V = A A ' . S A B C D = a 3 3 . a 2 3 2 = a 3 2
Đúng 0
Bình luận (0)
Cho hình thoi ABCD có AB=BD= 10 cm
1) Tam giác ABD là tam giác gì? Vì sao?
2) Tính số đo các góc của hình thoi ABCD
3) Tính độ dài AC
4) Tính diện tích hình thoi ABCD
1. Cho tam giác ABC vuông tại A, biết AB 9, AC 12a) Tính sinB, cosB, tanB, cotBb) Tính các tỉ số lượng giác của góc C1. Cho tam giác ABC vuông tại A, biết AB 9, AC 12a) Tính sinB, cosB, tanB, cotBb) Tính các tỉ số lượng giác của góc C2. Cho tam giác ABC vuông tại A,B 60 độ ; AB aa) Chứng minh: BC 2a; AC a căng3 . Tính số đo góc Cb) Tính các tỉ số lượng giác của góc B, góc C
Đọc tiếp
1. Cho tam giác ABC vuông tại A, biết AB = 9, AC = 12
a) Tính sinB, cosB, tanB, cotB
b) Tính các tỉ số lượng giác của góc C1. Cho tam giác ABC vuông tại A, biết AB = 9, AC = 12
a) Tính sinB, cosB, tanB, cotB
b) Tính các tỉ số lượng giác của góc C
2. Cho tam giác ABC vuông tại A,B =60 độ ; AB = a
a) Chứng minh: BC = 2a; AC = a căng3 . Tính số đo góc C
b) Tính các tỉ số lượng giác của góc B, góc C
Bài 2:
a: Xét ΔABC vuông tại A có
\(AB=BC\cdot\cos60^0\)
\(\Leftrightarrow BC=\dfrac{a}{\dfrac{1}{2}}=2a\)
\(\Leftrightarrow AC=\sqrt{BC^2-AB^2}=a\sqrt{3}\)
\(\widehat{C}=90^0-60^0=30^0\)
Đúng 0
Bình luận (0)
Cho tứ giác ABCD là hình thoi AC và BD giao nhau tại O có AB=6cm và B= 60 độ tính diện tích h thoi ABCD
Xem chi tiết
bạn tự vẽ hình nha ( mình nản vẽ hình lắm )
ta có AB = 6 cm
lại có góc ABC = 60 độ
suy ra : △ABC là △ đều ( △cân có một góc bằng 60 độ )
suy ra AC bằng 6 cm suy ra AO = CO = 3 cm
xét △ABO vuông tại O có :
theo định lý py-ta-go ta có AB2 = BO2+ AO2
=> BO2 = 36 - 9 = 25 (cm)
=> BO = 5 cm
=> BD = 10 cm
vậy diện tích hình thoi là:
1/2.6.10 = 30cm2 ( điều cần tìm )
Đúng 2
Bình luận (0)
1.Cho hình thoi ABCD có cạnh =a.Biết góc B=60 độ
a)C/m tam giác ABC đều
b)Tính diện tích hình thoi ABCD theo a
2.Cho hình vuông ABCD có độ dài cạnh =a.Điểm M bất kì trên đường thẳng AC.Kẻ ME vuông góc AB tại E và MF vuông góc AC tại F.Tìm vị trí của điểm M trên AC để diện tích tam giác CEF lớn nhất
1) hình tự vẽ nhé
a) Vì ABCD là hình thoi (gt)
\(\Rightarrow AB=BC\left(đn\right)\)
\(\Rightarrow\Delta ABC\)cân tại B
Mà \(\widehat{B}=60^0\)
\(\Rightarrow\Delta ABC\)là tam giác đều
b) Vì \(\Delta ABC\)đều(cmt)\(\Rightarrow AB=BC=AC=a\)
Gọi O là giao điểm 2 đường chéo BD và AC
Vì ABCD là hình thoi (gt) \(\Rightarrow DB\perp AC\left(tc\right)\)
\(\Rightarrow BO\perp AC\)
Vì tam giác ABC đều mà trong tam giác ABC thì BO là đường cao ứng với cạnh AC
\(\Rightarrow BO\)là đường trung tuyến ứng vs cạnh AC(tc)
\(\Rightarrow O\)là trung điểm của AC
\(\Rightarrow AO=OC=\frac{1}{2}AC=\frac{1}{2}a\)
Áp dụng định lý Py-ta-go vào tam giác BOC vuông tại O ta được:
\(BO^2+OC^2=BC^2\)
\(BO^2+\frac{1}{4}a^2=a^2\)
\(BO^2=\frac{3}{4}a^2\)
\(\Rightarrow BO=\frac{\sqrt{3}}{2}a\)
Ta có: \(S_{ABC}=\frac{1}{2}BO.AC=\frac{1}{2}.\frac{\sqrt{3}a}{2}.a\)
\(=\frac{\sqrt{3}}{4}a^2\)
CMTT \(S_{ADC}=\frac{\sqrt{3}}{4}a^2\)
\(S_{ABCD}=S_{ADC}+S_{ABC}=\frac{\sqrt{3}}{2}a^2\)

















