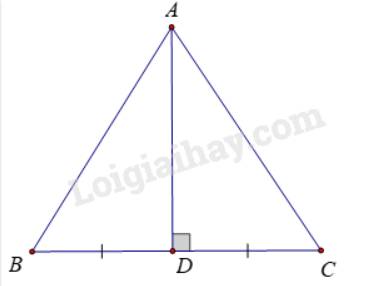
a) Kẻ đường trung trực của đoạn thẳng BC, cắt BC tại D

Ta có: Tam giác ABC cân nên AB = AC

\( \Rightarrow A\)thuộc đường trung trực của cạnh BC (t/c)

\( \Rightarrow AD\)là đường trung trực của BC.

Xét \(\Delta ABD\)và \(\Delta ACD\)có:

AB = AC (gt)

BD = CD (gt)

AD: cạnh chung

\( \Rightarrow \Delta ABD = \Delta ACD\left( {c - c - c} \right)\)

\( \Rightarrow \widehat {BAD} = \widehat {CAD}\)

\( \Rightarrow \)AD là tia phân giác góc BAC.

Vậy tam giác ABC cân tại A, đường trung trực của cạnh BC là đường cao và cũng là đường phân giác xuất phát từ đỉnh A của tam giác đó.

b)

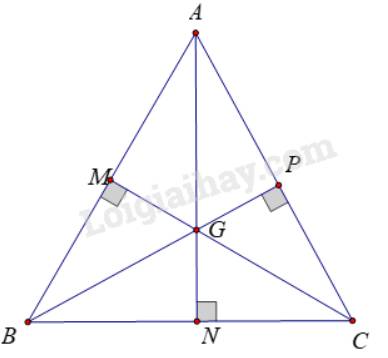
Ta có: Điểm cách đều ba đỉnh của tam giác là giao điểm ba đường trung trực của tam giác đó.

Tam giác ABC đều nên AB = BC = CA

Tam giác ABC cân tại A có AN là đường trung tuyến

\( \Rightarrow \) AN là đường phân giác xuất phát từ đỉnh A (cm ở ý a)

Tương tự: BP, CM lần lượt là đường phân giác xuất phát từ B và C của tam giác ABC

Mà AN cắt BP tại G

\( \Rightarrow G\) là giao điểm ba đường phân giác của tam giác ABC

\( \Rightarrow G\) cách đều ba cạnh của tam giác ABC (Tính chất

Tích chất đường trung trực. 1 điểm nằm trên đường trung trục thì cách đều 2 đầu mút của đoạn thẳng đó.

Thì tam giác cân luôn

Bài làm

Ví dụ: Cho tam giác ABC có nAH là đường trung trực. Chứng minh rằng: tam giác ABC cân tại A

Bài làm
Xét tam giác ABC có:

AH là đường trung trực

=> AB = AC ( tính chất đường trung trực của một tam giác )

Do đó: Tam giác ABC cân tại A ( đpcm )

# Học tốt #

1. Tính chất đường trung trực của một đoạn thẳng

Định nghĩa: Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng ấy tại trung điểm của nó.

Trên hình vẽ trên, $d$ là đường trung trực của đoạn thẳng $AB.$ Ta cũng nói: $A$ đối xứng với $B$ qua $d.$

Định lí 1: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.

Định lí 2: Điểm cách đều hai mút của đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.

$MA=MB$ $\Rightarrow$ M thuộc đường trung trực của $AB.$

Nhận xét:

Tập hợp các điểm cách đều hai mút của một đoạn thẳng là đường trung trực của đoạn thẳng đó.

2. Tính chất ba đường trung trực của tam giác

Định lí 1: Trong một tam giác cân, đường trung trực của cạnh đáy đồng thời là đường trung tuyến ứng với cạnh đáy này.

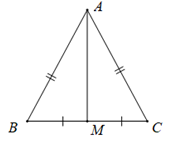
Định lí 2: Ba đường trung trực của một tam giác cùng đi qua một điểm. Điểm này cách đều ba đỉnh của tam giác đó.

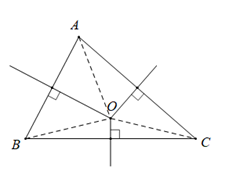
Trên hình, điểm $O$ là giao điểm các đường trung trực của $\Delta ABC.$ Ta có $OA=OB=OC.$ Điểm $O$là tâm đường tròn ngoại tiếp $\Delta ABC.$

a)Xét \(\Delta BEC\)vuông và \(\Delta BDA\)vuông, ta có:

Góc B : chung (gt)

Góc  BEC = Góc BDA (gt)

\(\Rightarrow\Delta BEC\infty\Delta BDA\left(g.g\right)\)

b) Xét \(\Delta DHC\)vuông và \(\Delta DCA\)vuông, ta có:

Góc D: chung (gt)

Cạnh DC: chung (gt)

\(\Rightarrow\Delta DHC\infty\Delta DCA\left(g.c\right)\)

\(\Rightarrow\frac{DH}{DC}=\frac{DC}{DA}\Rightarrow DC^2=DH.DA\)

c) Ta có: \(\Delta EAC\)vuông, áp dụng định lí Pytago:

\(EC=\sqrt{AC^2-AE^2}=\sqrt{100-64}=\sqrt{36}=6cm\)

Xét \(\Delta AHE\)vuông và \(\Delta CBE\)vuông, ta có:

Góc CEB = góc AEH (gt)

Góc CHD = góc AHE (2 góc đối đỉnh)

\(\Rightarrow\Delta AHE\infty\Delta CBE\left(g.g\right)\)

mà \(AE+EB=AB\Rightarrow EB=AB-AE=10-8=2cm\)

\(\Rightarrow\frac{HE}{BE}=\frac{AE}{CE}\Rightarrow EH=\frac{BE.AE}{CE}=\frac{2.8}{6}=\frac{8}{3}cm\)

ta có: \(CH+HE=CE\Rightarrow CH=CE-HC=6-\frac{8}{3}=\frac{10}{3}cm\)

Đây là toán lớp 5 nâng cao mà?

mình nghĩ đây ko phải là toán lớp 7

đây là toán lớp 7 đúng ko tích đi

hellooooooooooooooooooooo

- Tam giác cân là tam giác có hai cạnh bằng nhau.

- Tính chất: Trong một tam giác cân, hai góc ở đáy bằng nhau

- Các cách chứng minh một tam giác là tam giác cân:

   • Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.

   • Nếu một tam giác có hai cạnh bằng nhau thì tam giác đó là tam giác cân

- Tam giác cân là tam giác có hai cạnh bằng nhau.

- Tính chất: Trong một tam giác cân, hai góc ở đáy bằng nhau

- Các cách chứng minh một tam giác là tam giác cân:

   • Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.

   • Nếu một tam giác có hai cạnh bằng nhau thì tam giác đó là tam giác câ