cho tam giác ABC vuông tại A
vẽ AH vuông góc với BC (H thuộc BC)
lấy M thuộc AC,vẽ MN vuông góc với BC (N thuộc BC)
a, tìm góc = góc B
b, tìm góc = góc C
c, tìm góc bù với góc B
Những câu hỏi liên quan
Cho tan giác ABC vuông tại A vẽ AH vuông gócBC(H thuộc BC).lấy điểm M bất kì trên cạnh AC vẽ MN vuông góc BC(N thuộc BC)
a,tìm góc bằg gócB
b.tìm góc bù góc B
c.tìm góc bằng góc C
tam giác ABC cân tại A, góc A = 50 độ
a). Tính góc B, góc C
b). Vẽ AH vuông góc với BC (H thuộc BC). Chứng minh tam giác ABH = tam giác ACH
c). Biết AB = 17cm, BC = 16cm, tính AH
d). Vẽ CN vuông góc với AB (N thuộc AB), BM vuông góc với AC (M thuộc AC). Chứng minh NC = MB
aVẽ tam giác ABC.Qua A vẽ AH vuông góc với BC (H thuộc BC).Từ H vẽ HK vuông góc với AC (K thuộc AC);Qua A vẽ đường thẳng song song với B (cắt AB tại E)
bChỉ ra một cặp góc so le trong bằng nhau,1 cặp góc đối đỉnh bằng nhau
c Chứng minh :AH vuông góc với EK
dQua A vẽ đường thẳng m vuông góc với AH
CMR:m song song với EK
cho tam giác abc vuông tại A(AB<AC) vẽ AH vuông góc BC(H thuộc BC) D là điểm trên cạnh AC sao cho AD = AB Vẽ DE vuông góc với BC (E thuộc BC) DK vuông góc với AH tại K Chứng minh
a, AH = DK
b, Tam giác AHE vuông cân
Cho tam giác ABC, vẽ AH vuông góc với BC (H thuộc BC). Biết AB = 10cm, AH = 8cm, HC = 6cm
a) Tính AC và BH?
b) Chứng minh: góc ABC bằng góc ACB.
c) Vẽ HM vuông góc với AB, HN vuông góc với AC (M thuộc AB, N thuộc AC). Chứng minh: tam giác HMN là tam giác cân.
a, Theo định lí Pytago tam giác AHC vuông tại H
\(AC=\sqrt{AH^2+HC^2}=\sqrt{64+36}=10\)cm
Xét tam giác ABC có AB = AC nên tam giác ABC cân tại A
mà AH là đường cao đồng thời là đường trung tuyến
=> HC = HB = 6 cm
b, Vì tam giác ABC cân tại A => ^ABC = ^ACB
c, Vì tam giác ABC cân tại A, AH đồng thời là đường phân giác
=> ^BAH = ^HAC
Xét tam giác AMH và tam giác ANH có :
^AMH = ^ANH = 900
AH _ chung
^BAH = ^NAH ( cmt )
Vậy tam giác AMH = tam giác ANH ( ch - gn )
=> MH = NH ( 2 cạnh tương ứng )
Xét tam giác HMN có MH = NH ( cmt )
=> tam giác HMN cân tại H
Đúng 1
Bình luận (1)
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC (H thuộc BC). TÌm góc bằng góc B
Tham Khảo:
https://olm.vn/hoi-dap/detail/86010246553.html
Đúng 1
Bình luận (0)
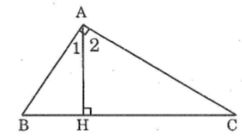
Có thể tìm góc B bằng hai cách:
Cách 1
Ta có: ∠(A1 ) + ∠(A2 ) = ∠(BAC) = 90o(1)
Vì ΔAHB vuông tại H nên:
∠B + ∠(A1) = 90o(tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra ∠B = ∠(A2 )
Cách 2
Vì ΔABC vuông tại A nên:
∠B +∠C = 90o (theo tính chất tam giác vuông) (1)
Vì ΔAHC vuông tại H nên:
∠(A2 ) + ∠C = 90o (tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra: ∠B = ∠(A2)
Đúng 0
Bình luận (1)
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC (H thuộc BC). Tìm góc bằng góc B.
Có thể tìm góc B bằng hai cách:
Cách 1
Ta có: ∠(A1 ) + ∠(A2 ) = ∠(BAC) = 90o(1)
Vì ΔAHB vuông tại H nên:
∠B + ∠(A1) = 90o(tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra ∠B = ∠(A2 )
Cách 2
Vì ΔABC vuông tại A nên:
∠B +∠C = 90o (theo tính chất tam giác vuông) (1)
Vì ΔAHC vuông tại H nên:
∠(A2 ) + ∠C = 90o (tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra: ∠B = ∠(A2)
Đúng 0
Bình luận (0)
cho tam giác ABC, vẽ về phía ngoài tam giác ABC các tam giác vuông tại A là tam giác ABD và tg ACE sao cho AB = AD, AC = AE.kẻ AH vuông góc với BC (H thuộc BC), DM vuông góc với AH(M thuộc AH), EN vuông góc với AH(N thuộc AH)
a) cm: DM =AH
b)cm MN đi qua trung điểm của DE
c)gọi K là trung điểm của BC. cm AK vuông góc với DE
Bạn vẽ hình ra nhé!
Do tam giác ABD vuông cân tại A => góc DAM + góc BAH = 90º. Trong tam giác vuông ABH có góc ABH + góc BAH = 90º => góc DAM = góc ABH (cùng phụ với một góc bằng nhau)
Xét tam giác vuông ADM và tam giác vuông BAH có:
AD = AB (gt)
góc DAM = góc ABH (cmt)
=> tam giác ADM = tam giác BAH (cạnh huyền - góc nhọn)
=> DM = AH
Cmtt ta có: tam giác ANE = tam giác CHA => EN = AH
=> DM = EN (cùng bằng AH)
Lại có: DM // EN (cùng _|_ AH) mà DM = EN (cmt) => tứ giác DMEN là hình bình hành => MN cắt DE tại trung điểm mỗi đường hay MN đi qua trung điểm của DE.
Chúc bạn học giỏi!
tk nha bạn
thank you bạn
(^_^)
Đúng 0
Bình luận (0)
Do tam giác ABD vuông cân tại A => góc DAM + góc BAH = 90º. Trong tam giác vuông ABH có góc ABH + góc BAH = 90º => góc DAM = góc ABH (cùng phụ với một góc bằng nhau)
Xét tam giác vuông ADM và tam giác vuông BAH có:
AD = AB (gt)
góc DAM = góc ABH (cmt)
=> tam giác ADM = tam giác BAH (cạnh huyền - góc nhọn)
=> DM = AH
Cmtt ta có: tam giác ANE = tam giác CHA => EN = AH
=> DM = EN (cùng bằng AH)
Lại có: DM // EN (cùng _|_ AH) mà DM = EN (cmt) => tứ giác DMEN là hình bình hành => MN cắt DE tại trung điểm mỗi đường hay MN đi qua trung điểm của DE.
Đúng 0
Bình luận (0)
Giúp mình với :Chứng minh rằng D=3x+3+3x+1+2x+3+2x+2 chia hết cho 6\(\)\(\varepsilon\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC (H thuộc BC). TÌm góc bằng góc B
Ta có:
góc BAH + góc HAC= 90độ (tam giác ABC vuông tại H)
Mà góc BAH + góc ABH =90độ (tam giác ABH vuông tại H)
=>góc ABH= góc HAC
Vậy góc B = góc HAC
Đúng 1
Bình luận (0)
cái tam giác mik vẽ là tam giác vuông cân nên góc B = góc C
nếu là tam giác thường thì khi đó:
kẻ đường thẳng sog song với AB đí qua H cắt AC tại K ( theo hibhf vẽ)
khi đó theo tính chất 2 đường thẳng song song sẽ có HK // BA
mà BA vuông góc tại AC( tam giác ABC vuông tại A)
=> HK vuông góc với AC
theo tính chất đồng vị => góc B = góc CHK
Đúng 1
Bình luận (0)