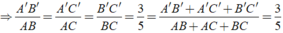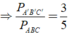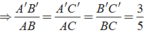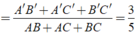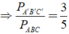cho tam giác A'B'C'~tam giác ABC theo tỉ số đồng dạng k=2/3. Tính tỉ số chu vi của 2 tam giác đó

Những câu hỏi liên quan
Cho tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số k = 4/3.Tính chu vi của tam giác ABC, biết chu vi của tam giác A'B'C' bằng 27 cm
tam giác A'B'C' đồng dạng tam giác ABC theo tỉ số đồng dạng k=\(\dfrac{2}{5}\)
a,tính tỷ số chu vi của 2 tam giác đã cho
b, cho biết hiệu chu vi của 2 tam giác trên là 30cm,tính chu vi của mỗi tam giác
`a) ΔA'B'C' ∼ ΔABC` theo tỉ lệ đồng dạng `k = 2/5`
`=> (A'B')/(AB) = (A'C')/(AC) = (B'C')/(BC) = 2/5`
Theo tính chất dãy tỉ số bằng nhau
`=> (A'B')/(AB) = (A'C')/(AC) = (B'C')/(BC) = (A'B' + A'C' + B'C')/(AB + AC + BC) = 2/5`
`=> (PΔA'B'C')/(PΔABC) = 2/5`
b) Từ a) ta có: `(PΔA'B'C')/(PΔABC) = 2/5`
`=> (PΔA'B'C')/2 = (PΔABC)/5`
Áp dụng tính chất dãy tỉ số bằng nhau:
`=> (PΔA'B'C')/2 = (PΔABC)/5 = (PΔABC - PΔA'B'C')/(5-2) = 30/3 = 10`
`=> PΔA'B'C' = 10 xx 2 = 20 (cm)`
`PΔABC = 10 xx 5 = 50 (cm)`
Đúng 0
Bình luận (0)
Cho tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số k
a) Tính tỉ số Chu vi của tam giác
b) Cho k= \(\dfrac{3}{5}\) và hiệu chu vi hai tam giác là 40dm.Tính chu vi mỗi tam giác
Lời giải:
a. $\triangle A'B'C'\sim \triangle ABC$ theo tỉ số $k$
$\Rightarrow \frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{A'C'}{AC}=k$
$\Rightarrow A'B'=kAB; B'C'=kBC; C'A'=kCA$
$\Rightarrow A'B'+B'C'+C'A'=k(AB+BC+AC)$
$\Rightarrow P_{A'B'C'}=kP_{ABC}$
$\Rightarrow \frac{P_{A'B'C'}}{P_{ABC}}=k$
b.
Chu vi tam giác ABC:
$40:(5-3).3=60$ (dm)
Chu vi tam giác A'B'C':
$40:(5-3).5=100$ (dm)
Đúng 1
Bình luận (0)
Cho tam giác đồng dạng với tam giác ABC theo tỉ số k = 4/3. Tính chu vi của tam giác ABC, biết chu vi của tam giác A'B'C' bằng 27cm.
Ta có Δ A'B'C' ∈ Δ ABC theo tỉ số k
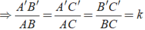
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
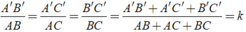
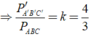
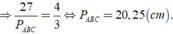
Đúng 0
Bình luận (0)
Đúng hay Sai
1. tam giác MNP đồng dạng EGF thì MN/NP = EG/FG
2. cho tam giác A'B'C' đồng dạng với tam giác ABC với tỉ số đồng dạng là k=2 khi đó tỉ số chu vi tam giác ABC so với chu vi tam giác A'B'C' là 2
Cho tam giác Δ A'B'C' ∼ Δ ABC theo tỉ số đồng dạng là k = 3/5. Tính tỉ số chu vi của hai tam giác đã cho.
Cho tam giác Δ A'B'C' ∼ Δ ABC theo tỉ số đồng dạng là k = 3/5. Tính tỉ số chu vi của hai tam giác đã cho.
Nhận định Đúng, Sai
1. tam giác ABC có BM là tia phân giác góc A thì AB/BC = AM/MC
2. Cho tam giác A'B'C' đồng dạng tam giác ABC với tỉ số đồng dạng k = 4 khi đó tỉ số chu vi tam giác A'B'C' so với chu vi tam giác ABC là 4
Cho 2 tam giác a'b'c' và abc đồng dạng theo tỉ số k. Chứng minh rằng tỉ số 2 chu vi tam giác cũng bằng k.
Cho tam giác Δ A'B'C' ∼ Δ ABC theo tỉ số đồng dạng là k = 3/5. Cho biết hiệu chu vi của hai tam giác trên là 40dm. Tính chu vi của hai tam giác đã cho