Hỏi nhiều quá , mà thà bạn nói ko cần vẽ hình thì còn giải , đằng này đã vẽ hình còn phải ghi GT , KL . mệt !!!!!!!!!!! @_@

Chứng Minh Định lý hai đường thẳng phân biệt cùng song song với đường thẳng thứ 3 thì chúng song song với nhau

ap sung ngay trong sach giao khoa ay doc lai di

Vẽ đường thẳng a//b vẽ c cắt a,b tại lần lượt hai điểm A, B( bạn tự vẽ hình ra nhé)

Vì a//b nên ta có:

aAB + bBc = 180 độ ( hai góc trong cùng phía)

Lại có:

Tia phân giác của aAb = 1/2 aAb

Tia phân giác của bBc = 1/2 bBc

=>1/2 aAb +1/2 bBc =1/2(aAb + bBc)

= 1/2 . 180độ

= 90 độ

Vì góc tạo bởi hai tia phân giác của cặp óc trong cùng phía bằng 90 độ nên chúng vuông góc với nhau

ta có: a//b => \(\widehat{A}+\widehat{B}=180^o\)

\(\widehat{A}_1+\widehat{B}_1=\frac{\widehat{A}}{2}+\frac{\widehat{B}}{2}=\frac{\widehat{A}+\widehat{B}}{2}=\frac{180^o}{2}=90^o\)

\(\widehat{O}=180^o-\left(\widehat{A_1}+\widehat{B_1}\right)=180^o-90^o=90^o\)

=> AO_|_BO tại O

tư đi mà vẽ hình

chứng minh 2 cặp góc đồng vị bằng nhau

=>2 tia phân giác cũng tạo nên 2 cặp góc đồng vị bầng nhau

=>nếu .....(DCCM)

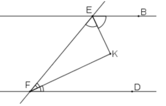
Giả sử đường thẳng AB // CD cắt đường thẳng EF tại E và F

Ta có: ∠BEF + ∠EFD = 180o (hai góc trong cùng phía)

+) Do EK là tia phân giác của góc ∠ BEF nên:

∠E1 = 1/2 .∠ (BEF) (1)

+) Do FK là tia phân giác của góc EFD nên :

∠F1 = 1/2 .∠EFD (2)

Từ (1) và (2) suy ra:

∠E1 +∠F1 =1/2 .(∠BEF + ∠EFD ) = 1/2 . 180º = 90º ( ∠BEF + ∠EFD = 180º hai góc trong cùng phía)

Trong ΔEKF,ta có:

∠EKF = 180o-(∠E1 + ∠F1) = 180o-90o=90o

Vậy EK ⊥FK